Hi, der Prof bei mir hatte in der VL ein Beispiel zum Thema AWP und ihren maximalen Lösungen gemacht. Das Beispiel, s.u..
Mein Problem ist, warum das maximale Definitionsintervall für b > 0 dieses eine I_max und für b < 0 das andere I_max ist. Ich dachte maximale Lösung des AWP heisst, die grösste Definitionsmenge der Lösung, also die grösste Menge aller t, die man einsetzen kann. Das wäre doch hier gerade eigentlich unabhängig ob jetzt b positiv oder negativ ist, die Vereinigung der beiden. Beispiel wenn b = 1 > 0 ist, sagen wir mal das AWP ist x‘(t) = x(t)^2 mit x(1) = 1 = b. Diese hat ja die Lösung x(t) = 1/(2-t). Dann muss ja hier der maximale Definitionsbereich gerade alle reelen Zahlen ausser t = 2 sein, also (-inf,2) U (2,inf). Nach seiner Interpretation wäre es aber hier ja wegen b > 0, (-inf,2). Das verstehe ich nicht.
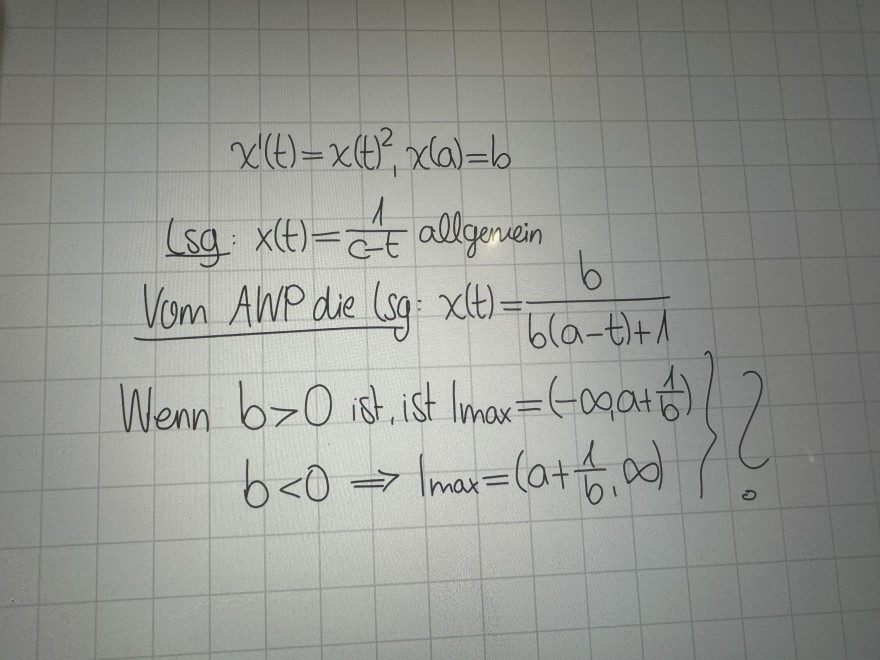
Text erkannt:
\( x^{\prime}(t)=x(t)^{2}, x(a)=b \)
\( \operatorname{lsg}: x(t)=\frac{1}{c-t} \) allgennein
Vom AWP die (sg: \( x(t)=\frac{b}{b(a-t)+1} \)
Wenn \( b>0 \) ist, ist \( \left.I_{\max }=\left(-\infty, a+\frac{1}{b}\right)\right\} \)
\( \left.b<0 \Rightarrow l_{\max }=\left(a+\frac{1}{b}, \infty\right)\right\}_{0}^{C} \)
Text erkannt:
\( x^{\prime}(t)=x(t)^{2}, x(a)=b \)
(sg: \( x(t)=\frac{1}{c-t} \) allgemein
Vom AWP die (sg: \( x(t)=\frac{b}{b(a-t)+1} \)
Wenn
\( \left.\begin{array}{l} x_{0}>0 \text { ist, ist } l_{\max }=\left(-\infty, a+\frac{1}{b}\right) \\ x_{0}<0 \Rightarrow l_{\max }=\left(a+\frac{1}{b}, \infty\right) \end{array}\right\} \int \limits_{0} \)