Was du da modelliert hast ist das gleichmäßige Abkühlen eines Stabes. Wenn das das ist, was du erreichen wolltest, dann hast du das richtig gemacht, mathematisch spricht auch nichts dagegen.
Den Rest solltest du also nur als reine Information lesen, dass ist keine Kritik an deinem Vorgehen.
Als Physiker sträubt sich aber etwas in mir: ein Gegenstand wird niemals linear abkühlen. Man muss z.B. überlegen, warum der Stab sich eigentlich abkühlt. Im absoluten Vakuum wird ein Stab seine Temperatur beibehalten, egal wie warm er ist.
Wenn er aber nicht im Vakuum liegt, dann muss die Energie an irgendetwas anderes abgegeben werden, allerdings hat dieses andere Objekt auch eine eigene Temperatur, die Abkühlung wird sich also nicht unendlich fortsetzen, sondern aufhören, wenn der Stab seine Umgebungstemperatur erreicht hat.
Das Newtonsche Abkühlungsgesetz besagt z.B., dass die Abkühlungsgeschwindigkeit in einem Luftstrom konstanter Temperatur proportional zur Temperaturdifferenz zwischen Luft und Gegenstand ist. Löst man die entstehende Differentialgleichung, dann erhält man einen exponentiellen Temperaturabfall, das heißt, anfangs fällt die Temperatur sehr stark und mit der Zeit wird sie immer langsamer.
Ich habe dazu mal einen Versuch gemacht, meine experimentell bestimmte Abkühlungskurve sah folgendermaßen aus:
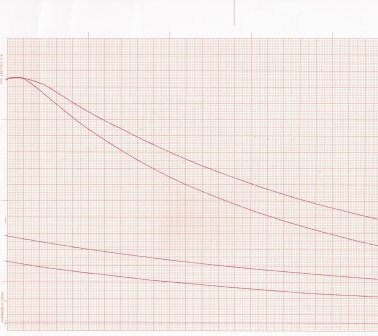
Die beiden Kurven beginnen bei der selben Anfangstemperatur, sind aber von zwei unterschiedlichen Körpern mit gleichem Volumen und gleichem Material. Der der schneller abkühlt hat aber eine größere Oberfläche, das Ziel war, eben diesen Einfluss nachzuweisen. (Die unteren beiden Kurven sind die gleichen wie die oberen, als das Blatt voll war ist der schreiber wieder nach links gesprungen und hat von dort weitergezeichnet.)
Einfach nur, damit du mal eine etwas realistischere Kurve siehst :-)