hier schon einmal die Beantwortung für Frage 1
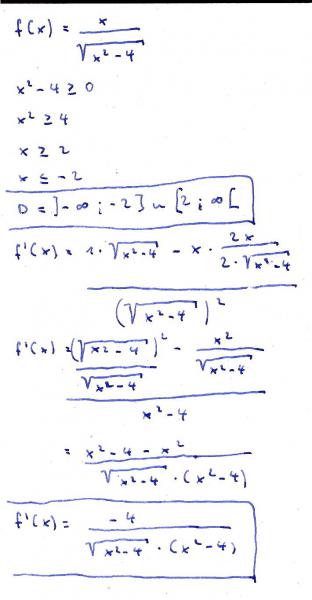

Nachtrag :
für beide Aufgaben wurde der Wertebereich und
die erste Ableitung gebildet.
Differenzierbar sind Funktionen falls die 1.Ableitung
auch eine Lösung hat ( im Def-Bereich der Funktion ).
Bei Aufgabe1. steht im Nenner der Ausdruck
x^2 - 4
Dieser darf nicht 0 sein ( Division durch 0 ).
x^2 - 4 <> 0
x <> 2
x <> -2
An diesen Punkten ist die Funktion nicht differenzierbar.
Bei Aufgabe2. steht im Nenner der Ausdruck
1 - x^4
Dieser darf nicht 0 sein ( Division durch 0 ).
1 - x^4 <> 0
x <> 1
x <> -1
An diesen Punkten ist die Funktion nicht differenzierbar.
Bei Fehlern oder Fragen wieder melden.
mfg Georg