quartische Funktionen Sekante = Tangente

Question

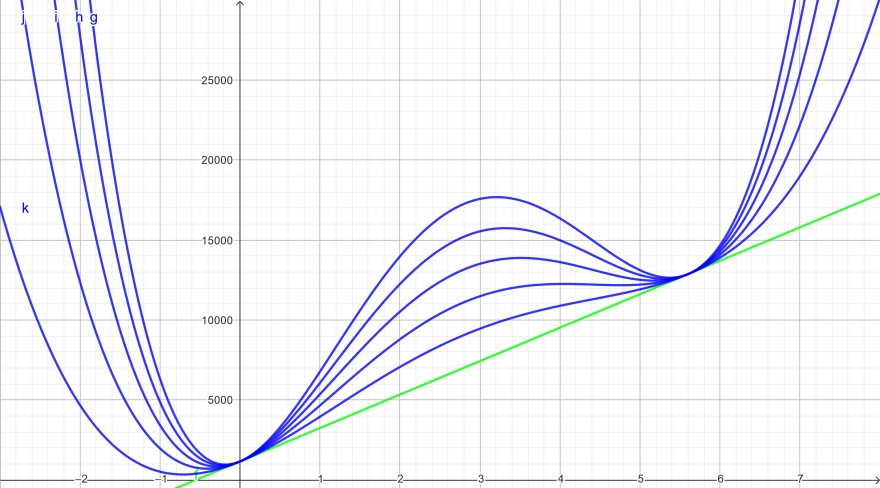
5 quartische Funktionen mit gleichen Abständen und Sekante = Tangente im Intervall 0 und 5,6

Hallo liebe Mathefreunde,

ich hoffe, dass ich heute an meinem Namenstag hier noch einmal zeigen darf, was ich noch berechnet und gezeichnet habe.

Weil Eurerseits nichts berechnet werden braucht / soll, hoffe ich, dass ich keinen Fehler mit diesem Post gemacht habe.

mit freundlichen Grüßen aus Wesertal

Martin Hümer

Comments

Ich sehe weder Sekanten noch den Sinn deines Posts.

---

Die Tangente ist gleichzeitig eine Sekante. Damit sieht das doch recht brauchbar aus.

Was gleiche Abstände hier bedeuten soll, ist mir allerdings unklar.

Da die Funktionen sich berühren, könnte man sagen, der Abstand ist 0.

---

folgende quartische Funktionen sind hier gezeichnet:

Text erkannt:

\( \begin{array}{l}\frac{200 x^{4}-2240 x^{3}+6272 x^{2}+6272 / 3 x+1159.2}{500 / 3 x^{4}-5600 / 3 x^{3}+15680 / 3 x^{2}+6272 / 3 x+1159.2} \\ \frac{400 / 3 x^{4}-4480 / 3 x^{3}+12544 / 3 x^{2}+6272 / 3 x+1159.2}{100 x^{4}-1120 x^{3}+3136 x^{2}+6272 / 3 x+1159.2} \\ \frac{200 / 3 x^{4}-2240 / 3 x^{3}+6272 / 3 x^{2}+6272 / 3 x+1159.2}{100 / 3 x^{4}-1120 / 3 x^{3}+3136 / 3 x^{2}+6272 / 3 x+1159.2} \\ \underline{6272 / 3 x+1159.2}\end{array} \)

für die erste quartische Funktion habe ich noch eine weitere Zeichnung erstellt:

Text erkannt:

GeoGebra Rechner Suite
Graflirechner
AUSTEILEN
annelden

---

In den nächsten 2 Zeichnungen sind jeweils 2 Flächen im Größenverhältnis 3 : 1 und dann noch als Flächengleichheit zu sehen.

Text erkannt:

GeoGebra Rechner Suite
Graflirechner
AUSTEILEN
annelden

Text erkannt:

GeoGebra Rechner Suite
V. Gmporgre
Alstmang
Mampev

Answer 1

Ich habe die quartische Funktion \(f(x)=(x-3)^4\) gewählt und diese dann um jeweils 1 Einheit nach oben verschoben. Somit haben die übereinanderliegenden Punkte immer 1 als Abstand. Die jeweiligen Tangenten immer die gleiche Steigung .

Comments

An der Skizze des Fragestellers kannst du besser erkennen, wie es gemeint war.