Wie komme ich auf Grenzerlös?

Question

Aufgabe:

Text erkannt:

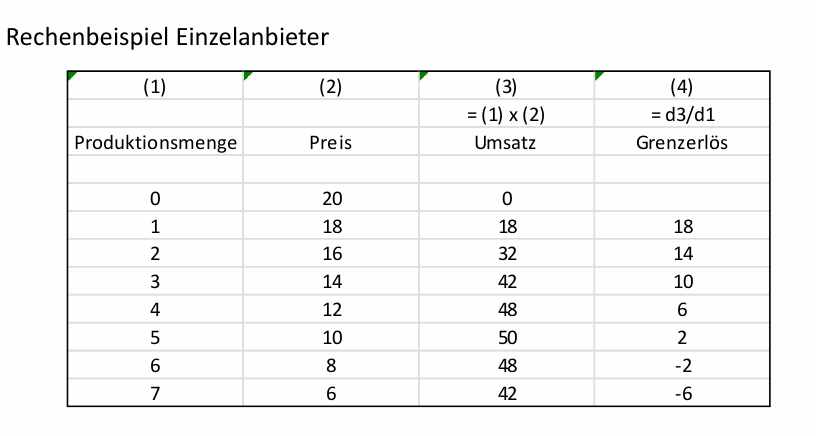
Rechenbeispiel Einzelanbieter
\begin{tabular}{|c|c|c|c|}
\hline\( (1) \) & \( (2) \) & \( (3) \) & \( (4) \) \\
\hline & & \( =(1) \times(2) \) & \( =\mathrm{d} 3 / \mathrm{d} 1 \) \\
\hline Produktionsmenge & Preis & Umsatz & Grenzerlös \\
\hline & & & \\
\hline 0 & 20 & 0 & \\
\hline 1 & 18 & 18 & 18 \\
\hline 2 & 16 & 32 & 14 \\
\hline 3 & 14 & 42 & 10 \\
\hline 4 & 12 & 48 & 6 \\
\hline 5 & 10 & 50 & 2 \\
\hline 6 & 8 & 48 & -2 \\
\hline 7 & 6 & 42 & -6 \\
\hline
\end{tabular}

Problem/Ansatz:

…  Wie komme ich auf die Grenzerlöse 10, 6, 2, -2, -6?

Comments

Die Werte in der Spalte 4 sind um eine Zeile zu viel nach unten gerutscht.

Bei einer Produktionsmenge von 0 beträgt der Grenzerlös 18, weil mit dem nächsten produzierten Stück ein Erlös (Umsatz) von 18 erzielt wird.

Answer 1

der Grenzerlös ist definiert als die Änderung des Umsatzes wenn eine weitere Einheit eines Gutes verkauft wird. Also hier:

18 - 0 = 18

32 -18 = 14

42 - 32 = 10

48 - 42 = 6

50 - 48 = 2

48 - 50 = -2

42 - 48 = -6

Immer den aktuellen Umsatz bei Menge x minus den davor bei Menge x-1.

Answer 2

Der Grenzerlös ist die Veränderung des Erlöses, also

18-0 = 18

32-18 = 14

42-32 = 10

usw.

Answer 3

Der Grenzerlös ist bei diesem Beispiel definiert als

\( \displaystyle g(x) = \frac{d}{dx} \;  \underbrace{\overbrace{x}^{\text{Produktionsmenge}}\cdot (\overbrace{20-2x}^{\text{Preis}})}_{\text{Umsatz}} = -4x + 20\)

wobei man in dieser Formel x, weil nur ganzzahlige Stückzahlen produziert werden, um 0,5 erhöhen muss.