Summe dritter Wurzeln ...

Question

Forme \( \sqrt[3]{11+4\sqrt{29}} \) + \( \sqrt[3]{11-4\sqrt{29}} \) in eine rationale Zahl um.

Answer 1

Mit \(u\coloneqq\sqrt[3]{11+4\sqrt{29}}\) und \(v\coloneqq\sqrt[3]{11-4\sqrt{29}}\) und \(w\coloneqq u+v\) gilt$$w^3=(u+v)^3=(u^3+v^3)+3uv(u+v)=22-21w.$$Daraus folgt$$(w-1)\cdot(w^2+w+22)=0.$$Die letzte Gleichung hat genau eine rationale Lösung, nämlich \(\boxed{w=1}\).

Comments

w ist aber nicht 1, sondern (3 \( \sqrt{29} \) + 1)/4 + (\( \sqrt{87} \) - \( \sqrt{3} \))/4*i

Die Aufgabe lautet doch: "forme den irrationalen Term in eine rationale Zahl um" - oder?

Dann ist 3*u*v nicht -21, sondern (-1)^(1/3)*21

daraus folgt w^3-22-21(-1)^(1/3)*w=0 -> bleibt komplex & irrational

Selbst wenn die Aufgabe lauten würde:
"Finde ein Polynom mit rationalen oder ganzzahligen Faktoren, dessen Nullstelle mit diesem gegebenen Term übereinstimmt"

wäre die Lösung:

484 - 22 x - 21 x^2 - x^3 + x^4=0

oder 484 + x (-22 + x (-21 + (-1 + x) x))=0

Hierbei ist eine der 4 komplexen Nullstellen = w

Oder ist die Aufgabenstellung unvollständig? Oder anders gemeint?

---

Das hatte ich schon in meiner Antwort angesprochen.

Die dritte (allgemein ungerade) Wurzel aus einer negativen Zahl betrachten manche als definiert, z.B. \( \sqrt[3]{-8} \) = -2, da \( (-2)^{3} \) = -8.

Nur dann funktioniert die Umformung.

Allerdings gelten dann die üblichen Potenzregeln nicht mehr, daher halte ich es mit denen, die sagen, Wurzeln aus negativen Zahlen sind generell nicht definiert und dann ist bereits der zweite Term im vorgegebene Ausdruck nicht definiert, Umformungen kann man sich dann natürlich schenken.

Insofern ist die Aufgabe entweder banal oder falsch. Man suche es sich aus.

---

Also wenn solche Trickserei als richtig angesehen wird, wo aus einer komplexen irrationalen Zahl eine einfache reelle Zahl "hingebastelt" wird, bin ich raus.

Da versagt jegliche Kontrolle.

Beispiel:

der echte Term w: Re(w^3)= 65/2

Der hier als "beste Antwort betrachtete w=1": Re(w^3) = 1

Das ist eine andere Mathematik... oder ich bin im falschen Forum.

---

... oder ich bin im falschen Forum.

sehe es einfach so: nobody ist perfect.

Und wäre die Frage nicht korrekt gestellt, wenn Roland nach $$\sqrt[3]{4\sqrt{29}+11} - \sqrt[3]{4\sqrt{29}-11} $$gefragt hätte?

Answer 2

Wenn man die dritte Wurzel aus einer negativen Zahl als definiert ansieht, kommt als Ergebnis die kleinste natürliche Zahl heraus.

Answer 3

Man kann den Term solange umformen, bis Real- & Im-Teil nur noch irrationale Zahlen sind:

Irrational, weil Wurzeln aus Primzahlen immer irrational sind.

Und irrational bedeutet: nicht rational darstellbar!

Man kann sich nur näherungsweise auf N Stellen herantasten -> wird aber den exakten Wert NIE erreichen:

Comments

Darf man fragen, was Du hier gerechnet hast?

---

Vermutlich wollte er die Wurzel aus einer negativen Zahl ziehen und hat dann eine komplexe Zahl heraus bekommen.

Beachte, dass die Wurzel aus einer negativen Zahl nicht umsonst von Mathematikern eigentlich nicht definiert ist.

---

Die Aufgabenstellung klingt etwas unlogisch oder unfertig.

Eine logische Aufgabenstellung wäre z.B.:

"Ändere den gegebenen Term leicht so um, dass eine Rationale Zahl herauskommt."

Gegeben war also die irrationale komplexe Zahl w.

Wenn man diese mit 3 potenziert und nur den Realteil betrachtet:

Re(w^3) = 65/2 ->  dann ist das eine

https://de.wikipedia.org/wiki/Rationale_Zahl

P.S.: aus Zeitgründen kontrolliere ich alles per Mathematica

---

@hyperG: Tut mir leid für deine verschwendete Zeit. Vielleicht hättest du vorher wissen sollen, dass Rolands Fragen meistens mindestens einmal nachgebessert werden müssen.

Aber da etwas Rationales herauskommen soll, sollte klar sein, dass sicherlich keine komplexe Zahl mit der Wurzel aus einer negativen Zahl gemeint sein kann.

Denn eine komplexe Zahl lässt sich nicht zu einer rationalen Zahl umformen.

---

Ich habe die Aufgabe so verstanden, dass die dritte Wurzel als Umkehrfunktion der reellen Funktion \(x \mapsto x^3\) gemeint ist und somit wohldefiniert ist. Dann kann man die Aufgabe durch Bestimmung der benötigten dritten Wurzeln lösen:

$$\left(\frac{1}{2}(1+\sqrt{29})\right)^3=11+4\sqrt{29}$$

$$\left(\frac{1}{2}(1-\sqrt{29})\right)^3=11-4\sqrt{29}$$

PS: Die Kritik an der Fragestellung finde ich überzogen.

@Mathecoach: Eine mathematische Untersuchung macht stets Freude und ist niemals "verschwendete Zeit".

---

Das mit der dritten Wurzel sehe ich genauso. Die Fragestellung ist insofern schlecht formuliert, weil eine Zahl durch Umformungen nicht ihren Wert ändert. Eine korrekte Formulierung wäre z.B. "Zeige durch Umformung, dass ... eine rationale Zahl ist".

---

Wir reden aneinander vorbei:

ich kritisiere nicht,

- dass die 3. Wurzel einer negativen reellen Zahl nach Potenzieren mit 3 negativ reell sein kann

- dass ((1 - Sqrt[29])/2)^3 =11-4*\( \sqrt{29} \)  ist

- dass u^3+v^3 =22 ist

sondern, dass bei

(3 u^2 v + 3 u v^2)/(u + v) = 3*u*v

einfach der komplexe Anteil ignoriert wurde und -21 als reelle Zahl hingeschrieben wird, als wenn (-1)^(1/3) = -1 wäre

statt sauber +21*(-1)^(1/3) = 21/2 + 21/2* \( \sqrt{3} \) * i

=10.5000000000000 + 18.1865334794732... i

zu rechnen

siehe https://www.justmaththings.de/de/reference/ComplexPower

Der komplexe Anteil kürzt sich nur bei ganzzahligen Potenzen heraus:

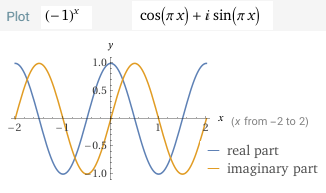
(siehe auch

https://de.wikipedia.org/wiki/Elektrische_Impedanz

)

Kontrolle mit Dezimalschreibweise und primitiver Addition:
u= 3.19258240356725...

v= 1.09629120178363... + 1.89883206137998... i

u+v = 4.28887360535088... + 1.89883206137998... i

Noch was zu (-8)^(1/3): dieser Term hat eigentlich 3 Interpretationen:

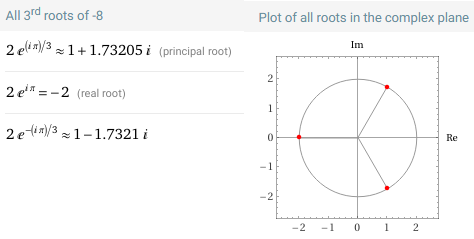
Einfach nur ein Term zu betrachten, der einem gefällt -> und dann jegliche Kontrolle zu ignorieren {Re(w^3)} -> wird immer zu Folgefehlern führen.

Vermutlich müsste die Fragestellung so lauten:
"Der gegebene Term w hat wegen der 3. Wurzel einer negativen Zahl 3 Interpretationen für Zwischenergebnisse (ohne Folgerechnungen):

Finde eine der 3 Interpretationen, die reel ohne komplexen Anteil sind."

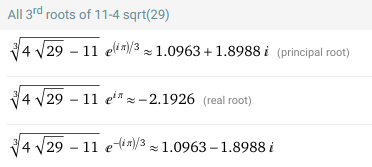
Davon pickt man sich die 2. Interpretation heraus, rechnet

3,19... -2,19... = 1 fertig.

---

Eben. Mit dem Unterschied, dass einge von uns aus dem Kontext auf eine intendierte Interpretation der Wurzel geschlossen haben - übrigens bei beiden Termen.

---

Du schaffst Dir die Probleme erst selber durch Ausweitung der Fragestellung auf die komplexen Zahlen.

Und ja \( \sqrt[3]{-1} \) = -1 da (-1)³ = -1

Zumindest für die, die sich nicht daran stören, dass dann allerdings  \( (-1)^{1/3} \) ≠  \( (-1)^{2/6} \)