Zusammenhang zwischen dritter Wurzel und Quersummen? Beispiel: ³√512 = 8 = 5 + 1 + 2

Question

Heute habe ich dieses Konstrukt auf Facebook gesehen:

$$\sqrt[3]{0} = 0 \\\sqrt[3]{1} = 1 \\\sqrt[3]{512} = 8 = 5 + 1 + 2 \\\sqrt[3]{4913} = 17 = 4 + 9 + 1 + 3 \\\sqrt[3]{5832} = 18 = 5 + 8 + 3 + 2 \\\sqrt[3]{17576} = 26 = 1 + 7 + 5 + 7 + 6 \\\sqrt[3]{19683} = 27 = 1 + 9 + 6 + 8 + 3$$

Ist das "zufällig", sozusagen gut gefunden? Oder kann man daraus ggf. eine Formel herleiten, die die dritte Wurzel und die Quersumme in Verbindung bringt?

Anders ausgedrückt: Es geht um mit 3 potenzierte Werte, deren Quersumme wieder die Basis ergibt. $8^3 = 512 → 5+1+2 = 8$

Answer 1

Hallo Kai,

$Q(n)$ sei die Quersumme von $n$ im 10'ner-System. Wenn man alle Zahlen $n$ im Intervall $n \in [0; 2097151]$ durchprobiert, und prüft ob $Q(n^3) = n$ ist, so findet man genau die 7 Treffer $n \in \{ 0, 1, 8, 17, 18, 26, 27 \}$. Und darüber hinaus wird es auch keine Zahl $n$ mit dieser Eigeschaft mehr geben, da die Quersumme von $Q(n^3)$ sehr viel langsamer wächst als $n$. Folgendes Bild zeigt das mit $n \le 100$:

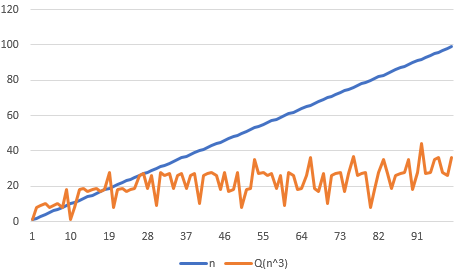
So gesehen ist der Zusammenhang eher 'zufällig'. Es gilt das 'Gesetz der kleinen Zahlen'. Es gibt so wenige davon, daher kommt es vor, dass zwei aus unterschiedlichen Mengen (hier $Q(n^3)$ und $n$) auch mal gleich sind.

Comments

Das verstehe ich unter einer eindeutigen, klar verständlichen Antwort. Perfekt.

---

@Kai: Ich schließe mich deiner Bewertung an. Und was sagst du zu den "Synonymen" "zufällig", und "gut gefunden"?

Answer 2

"zufällig", und "gut gefunden" sind keine Synonyme. Wenn man ein Programm schreibt, das für a₁,a₂, ... a_n∈{0,1,2,3,4,6,6,7,8,9} prüft, ob (a₁+a₂+...+a_n)³=10^n-1·a₁+10^n-2·a₂+ ... +a_n gilt, dann findet dies Programm deine Lösungen keineswegs "zufällig", sondern ganz gezielt.

Comments

Danke. Stimmt genau. Werners Grafik, die er mit einem Programm entworfen hat, hat mir vor Augen geführt, dass es nur für wenige Zahlen klappt.