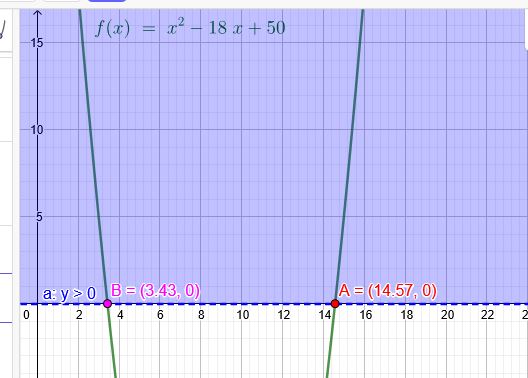
\( 18 n<n^{2}+50\)
\( n^{2}+50>18 n|-18n\)
\( n^{2}-18n+50>0|-50\)
\( n^{2}-18n>-50\) quadratische Ergänzung \(+ (\frac{18}{2})^2 \)
\( n^{2}-18n+ (\frac{18}{2})^2>-50+ (\frac{18}{2})^2\) 2. Binom
\( (n-\frac{18}{2})^2>31|±\sqrt{~~}\)
1.)
\( n-9>\sqrt{31}\)
\( n_1>9+\sqrt{31}≈14,58\)
2.)
\( n-9<\red{-}\sqrt{31}\)
\( n_2<9-\sqrt{31}≈3,43\)
Lösungen: \( n_1>9+\sqrt{31}\) oder \(n_2<9-\sqrt{31}\)