Die Aufgabe lautet nun:
Die Fläche zwischen K und den Koordinatenachsen im 4. Feld (also im 4. Quadranten) soll ein größtmöglichstes viereck mit dem Eckpunkt A(0|-2) einschließen. Bestimmen Sie das Viereck mit der größtmöglichen Fläche.
Skizze:
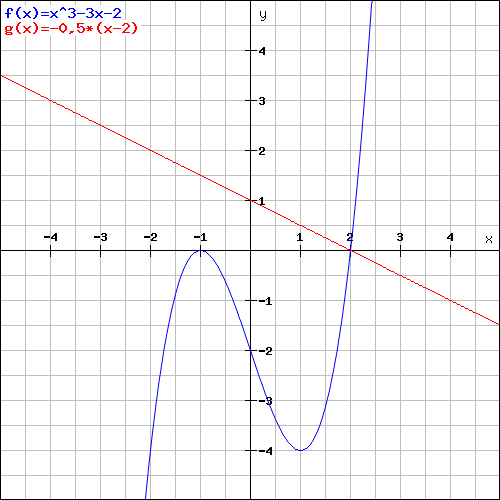
Meiner Meinung nach gibt es hier nur die Möglichkeit mit D(0|0)
f(x) = x^3 - 3x - 2 = -2
x^3 - 3x = 0
x(x^2 - 3) = 0
x1 = Wurzel(3)
Andere Lösungen nicht interessant
f(Wurzel(3)) = 3^{3/2} - 3+3^{1/2} - 2 = 4√3-5
Also B(4√3-5 | -2) und C(4√3-5 | 0)
Die Gerade hat hier doch eigentlich überhaupt keine Auswirkungen.