um gleich vorneweg zu Fragen: Gibt es für die Zielfunktionen irgendwelche Regeln, da diese sich ja nach Struktur bzw. der vorliegenden Flächenform richten?
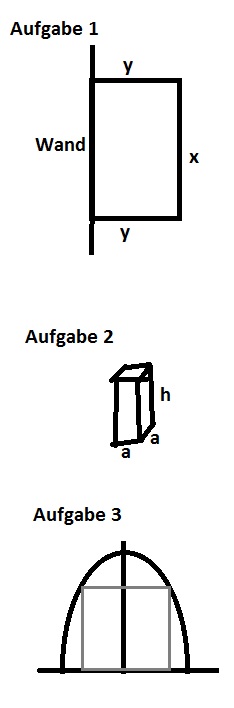
Aufgabe 1: An einer Garagenwand soll ein rechteckiges Kräuterbeet abgegrenzt werden. Es stehen 30m Maschendrahtzaun zur Verfügung. Berechne die Ausmaße, Länge, Breite und wann die Fläche des Beetes maximal wird.
Zulässiger Bereich: y + x = maximal 30 (Siehe Skizze unten)
2y + x = 30 | -2y
x = 30 - 2y Einsetzen in Zielfunktion A(x) = x * y
A(x) = (30 - 2y) * y
= 30y - 2y^2 | : ( -2)
= y^2 - 15y
Nullstellen 1. Ableitung berechnen
A'(x) = 2y - 15 = 0 |+15
2y = 15 | :2
y = 7,5
2. Ableitung und Extremstelle berechnen
A ' ' (7,5) = 2 > 0 (Tiefpunkt)
x Berechnen: 30-2*7,5 = 15m max. Volumen: 7,5*15=112,5 m^3
Aufgabe 2: Aus einem Stück Draht, das 36cm lang ist wird eine Säule mit quadratischem Grundriss geformt. Wie groß ist das maximal mögliche Volumen der Säule.
Zulässiger Bereich: a und h verlaufen von 0 bis max 36cm (Skizze siehe unten)
8a + 4h = 36 Zielfunktion für Volumen der Säule: v(x) = a^2 * h
8a+4h =36 |-8a
4h = 36 - 8a |:4
h = 9 - 2a
Berechne 1. Ableitung und Nullstellen: v ' (x) = -6a^2+18a x1=0 x2=3
Berechne 2. Ableitung für HP und TP v ' ' (x) = -12a+18
v''(0) = -12*0+18 = 18 > 0 TP
v''(3) = -12*3+18 = -18 < 0 HP
Berechne das Seitenverhältnis:
h=26-8*3:4=3
a=36-4*3:8=3
Berechne Volumen nach a*a*h = 3*3*3 = 27 cm^2 (Würfelform)
Aufgabe 3: Einer Parabel mit der Funktionsgleichung f(x)=4-x^2 soll im ersten Quadranten ein Rechteck mit maximalem Flächeninhalt einbeschrieben werden. Gesucht sind Breite, Höhe und Flächeninhalt dieses Rechtecks.
f(x) = -x^2+4
f(x1) = a * b = 2 * x1 * f(x1)
A(x) = 2 * x1 * (-x^2+4)
A(x) = -2 * x1^3 + 8*x1
1. Ableitung
A ' (x1) = -6x^2+8 = 0 x1 = 1,15 x2 = -1,15
2. Ableitung A '' (x1) = -12x
A''(1,15) = -12 * (1,15) = -13,8 < 0 HP
A''(-1,15) = -12 * (-1,15) = 13,8 > 0 TP
maximale Fläche: Amax = -2 * (1,15)^3 + 8 * (1,15) = 6,15
Ich bedanke mich für jeweilige Korrekturen im voraus, denn es wird wohl zu finden geben.
MfG