Hi,
die gesuchte Folge kann man wie folgt konstruieren. Man fängt bei 0 an und geht einen Schritt mit der Schrittweite 1 nach rechts. Sobalb man den Wert 1 erreicht hat, geht man in die andere Richtung nach 0 mit einer halbierten Schrittweite. Das bedeutet das die neue Schrittweite nun 1/2 ist und die nächsten Folgenwerte sind 1/2 und 0. Sobald die linke Grenze 0 erreicht wird kehrt man wieder um in Richtung 1 und zwar wieder mit halbierter Schrittweite, aslo mit 1/4. Damit ergeben sich die Folgenwerte 1/4, 1/2, 3/4 und 1. Jetzt wieder umkehren mit Schrittweit 1/8 usw.
Es ergibt sich folgende Folge 0, 1, 1/2, 0, 1/4, 1/2, 3/4, 1, 7/8, 3/4, 5/8, ... Das ganze kann man in dem folgenden Bildungsgesetz zusammenfassen $$ a_0=0 \quad a_1=1 \text { und } a_{2^n+k-1}=a_{2^n-1}+ \left(-\frac{1}{2}\right)^nk \text { für } k=1,..2^n$$
Die Folge ist beschränkt, da die Folgenwerte sich alle im Bereich [0, 1] befinden. Zwei aufeinander folgende Folgenwerte haben einen Abstand von $$ \left( \frac{1}{2} \right)^n $$ und streben damit gegen Null, bzw. zu jedem $$ \epsilon > 0 \text { gibt es ein } n_0 \text { s.d. für alle } n>n_0 \text { gilt } \left|a_{k+1}-a_k\right|<\epsilon $$ Die Folge ist divergent da sie zwei Häufungspunkte hat, nämlich 0 und 1. Damit hat man eine Folge mit den gewünschten Eigenschaften konstruiert.
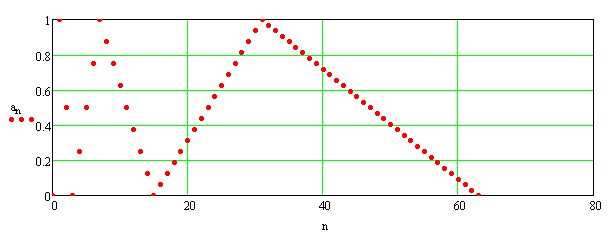
Der Folgenverlauf ist aus dem beigefügten Bild zu erkennen. In dem Beispiel läuft n=0,..5