Kurvendiskussion. Stimmt meine Rechnung?

Question

f(x)= x³-6x²+9x 

f'(x)= 3x²-12x+9 

f''(x)= 6x-12 

f'''(x)= 6 

Symmetrie

Keine Symmetrie, denn es tauchen gerade und ungerade Exponenten auf. 

Nullstellen

x(x²-6x+9) 

x₁=0 

x₂=3

Extrema

3x²-12x+9=0 |:3 

x²-4x+3=0 

x₁=3

x₂=1 

f''(3)= 6x-12 = 6 

f''(1)= 6x-12 = -6 

H(1|4) T(3|0)

Wendestellen

6x-12=0 |+12 

6x=12 |:6 

x= 2 

f'''(2)= ≠ 6 

W(2|2)

Definitionsbereich

D=ℝ 

Verhalten für x → ∞ 

x → ∞:f(x)= ∞

x ∞ -∞:f(x)= -∞

Monotonie Verhalten

f'(x)= > 0  Streng monoton steigend. 

f'(x)= < 0 Streng monoton fallend. 

3x²-12x+9=0 |:3

x²-4x+3=0 

x₁=3

x₂= 1 

Die Funktion ist bei f' Streng monoton Steigend. 

Skizze: 

 

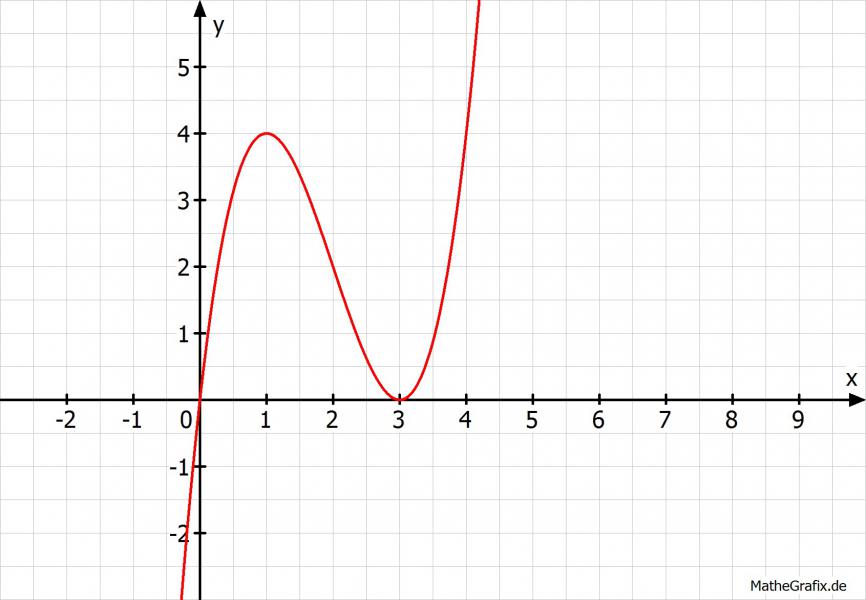
Bei dieser Funktion kann ich doch keine Polstellen oder Asymptoten berechnen oder? 

Ich hoffe der Rest stimmt. 

Answer 1

Die Untersuchung des Monotonieverhaltens stimmt nicht. Bzw. die Schlussfolgerung

Mononton steigend für x <= 1 oder x >= 3

Monoton fallend für 1 <= x <= 3

Ansonsten ist das richtig.