Hi,
bestimme zuerst die Ableitungen:
f(x) = 1/6*x^3-3/4*x^2+2
f'(x) = 1/2*x^2-3/2*x
f''(x) = x-3/2
f'''(x) = 1
Wendepunkt: f''(x) = 0
x = 3/2
Überprüfen mit f'''(3/2) ≠ 0.
Einsetzen in f(x) -> f(3/2) = 0,875
Wir haben den Wendepunkt mit W(3/2|0,875) erkannt.
Nun die Tangente dazubestimmen. Ableitung in der Stelle x = 3/2 bestimmen, das entspricht dann auch der Steigung der Tangente.
f'(3/2) = m = -1,125
Nun in die allgemeine Gleichung einer Gerade W und m einsetzen: y = mx+b
0,875 = -1,125*3/2+b
b = 2,5625
Die gesuchte Tangente lautet also y = -1,125*x + 2,5625
Kontrolle mit Schaubild:
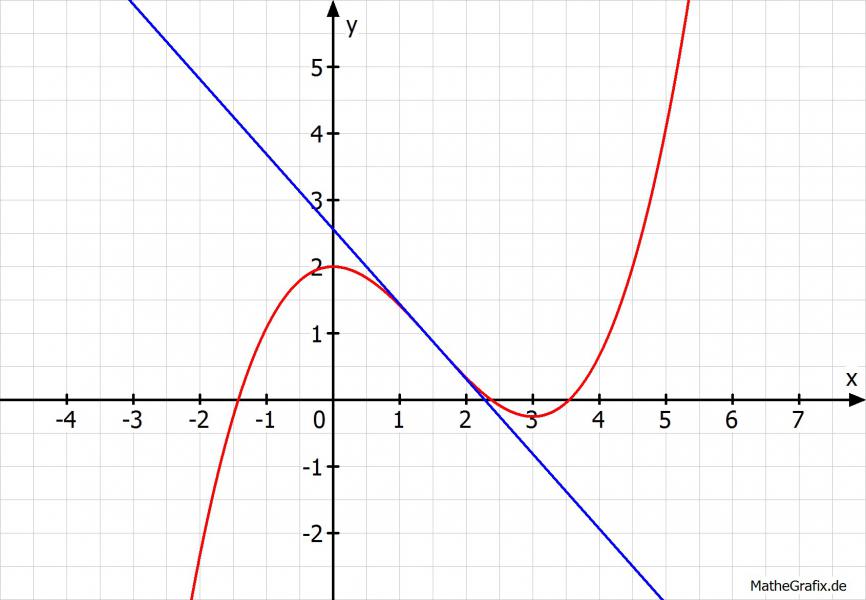
Grüße