wie finde ich eine Tangente, die ein Schaubild senkrecht schneidet?

Question

hi,

ich habe eine Aufgabe, die ich nicht lösen kann:

gegeben ist eine gerade g mit g(x)= -3/2x-2 , K1 mit f(x)= 1/10x^3+1/5x^2-3/2x, K2 mit y=2/15x^2+2/3x,

so, nun soll ich die Gleichung einer Tangente bestimmen, welche an K1 liegt, parallel zu g verläuft und K2 senkrecht schn eidet...


Hilfe!

Answer 1

Nun, die gesuchte Tangente

t ( x ) = m x + b

muss folgende Eigenschaften haben:

A) t verläuft parallel zu g, also

t ' ( x ) = g ' ( x ) <=> m = - 3 / 2

 

B) An einer Stelle x₀ (Berührstelle von t und f ) muss gelten:

t ' ( x₀ ) = f ' ( x₀)
und
t ( x₀ ) = f ( x₀)

Aus der ersten Gleichung ergibt sich:

t ' ( x₀ ) = f ' ( x₀)

<=> - 3 / 2 = ( 3 / 10 ) x₀² + ( 2 / 5 ) x₀ - ( 3 / 2 )

<=> 0 = ( 3 / 10 ) x₀² + ( 2 / 5 ) x₀

<=> x₀ ( ( 3 / 10 ) x₀ + ( 2 / 5 ) ) = 0

<=> x₀ = 0 oder ( 3 / 10 ) x₀ + ( 2 / 5 ) = 0

<=> x₀ = 0 oder ( 3 / 10 ) x₀ = - 2 / 5

<=> x₀₁ = 0 oder  x₀₂ = - 4 / 3

An diesen beiden Stellen haben t und f die gleiche Steigung. Damit diese Stellen auch Berührpunkte von t und f sind, müssen dort auch die Funktionswerte von t und f übereinstimmen, also (siehe zweite Gleichung):

- ( 3 / 2 ) x + b =  ( 1 / 10 ) x ³ + ( 1 / 5 ) x ² - ( 3 / 2 ) x

<=> b = ( 1 / 10 ) x ³ + ( 1 / 5 ) x ²

Daraus ergibt sich für x₀₁ = 0:

b₁ = ( 1 / 10 ) x₀₁³ + ( 1 / 5 ) x₀₁² 

= ( 1 / 10 ) * 0 ³ + ( 1 / 5 ) * 0 ²

= 0

und für x₀₂ = - 4 / 3 :

b₂ = ( 1 / 10 ) x₀₂³ + ( 1 / 5 ) x₀₂² 

= ( 1 / 10 ) * ( - 4 / 3 ) ³ + ( 1 / 5 ) * ( 4 / 3 ) ²

= ( - 64 / 270 ) + ( 16 / 45 )

= ( - 64 / 270 ) + ( 96 / 270 ) = 32 / 270

= 16 / 135

Somit ergeben sich die beiden folgenden Tangenten an K1, die parallel zu g verlaufen:

t₁ ( x ) = ( - 3 / 2 ) x

t₂ ( x ) = ( - 3 / 2 ) x + ( 16 / 135 )

 

C) Nun muss noch die Bedingung erfüllt werden, dass die Tangente den Graphen von K2 senkrecht schneidet. Dazu muss es eine Stelle x₂ geben, an der die Steigung von K2 gleich dem negativen Kehrwert der Steigung von t₁ bzw. t₂ ist, an der also gilt:

K2 ' ( x₂ ) = - 1 /  t₁ ( x₂ ) bzw. K2 ' ( x₂ ) = - 1 / t₂ ( x₂ )

Außerdem müssen dort die Funktionswerte von K2 und t₁ bzw. t₂ übereinstimmen.

Da t₁ und t₂ die gleiche Steigung haben, braucht man nur einmal zu rechnen:

K2 ' ( x₂ ) = - 1 /  t₁ ( x₂ )

<=> ( 4 / 15 ) x₂  + ( 2 / 3 ) = 2 / 3

<=> ( 4 / 15 ) x₂ = 0

<=> x₂ = 0

Also: Nur an der Stelle x₂ = 0 hat K2 dieselbe Steigung wie die beiden Tangenten t₁ bzw. t₂.

Prüfung der Funktionswerte:

K2 ( 0 ) = 0 = t₁ ( 0 )

t₁ schneidet also K2 an der Stelle x₂ = 0. Da t₁ und t₂ verschieden sind, kann t₂ den Graphen von K2 nicht auch an der Stelle x₂ = 0 schneiden.

Also:

Nur die zu g parallel verlaufende Tangente an K1 mit der Gleichung

t₁ ( x ) = - ( 3 / 2 ) x

schneidet den Graphen von K2 an der Stelle x₂ = 0 senkrecht und erfüllt somit die Forderungen der Aufgabenstellung.

 

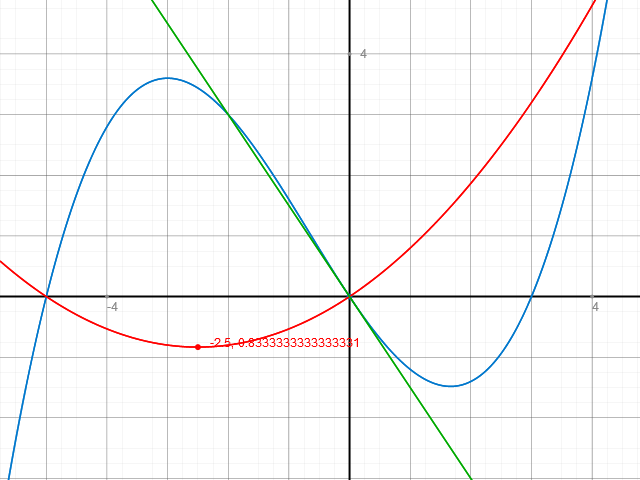
Hier noch die Graphen von K1,  K2 und t₁ :