um die Funktionsgleichungen zu bestimmen, stellen wir einfach nach y um:
x = 3y - 7 | 3y = x + 7 | y = 1/3 * x + 7/3
x = 2y - 2 | 2y = x + 2 | y = x/2 + 1
Wo schneiden sich die Geraden? Gleichsetzungsverfahren:
1/3 * x + 7/3 = x/2 + 1 | - 1/3 * x
7/3 = x/2 - 1/3 * x + 1 | - 1
4/3 = x/2 - 1/3 * x
4/3 = 3/6 * x - 2/6 * x = 1/6 * x | * 6
24/3 = 8 = x
Nun x = 8 in eine der Funktionsgleichungen einsetzen, um y zu bestimmen:
8 = 3y - 7 | + 7
15 = 3y
y = 5
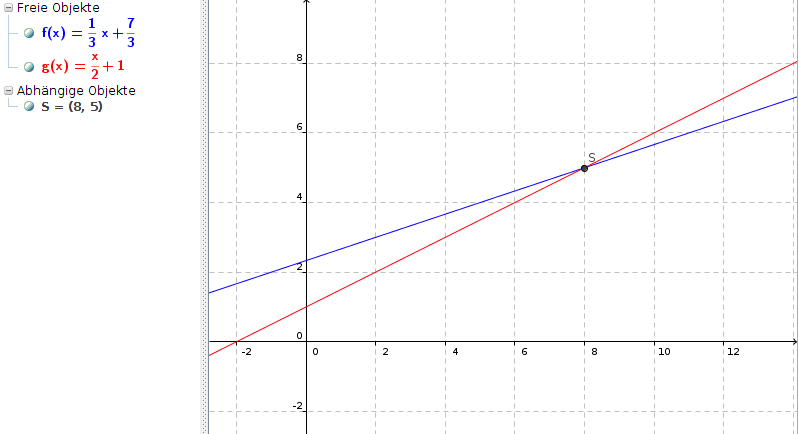
Der Schnittpunkt der beiden Geraden lautet (8|5)
Besten Gruß