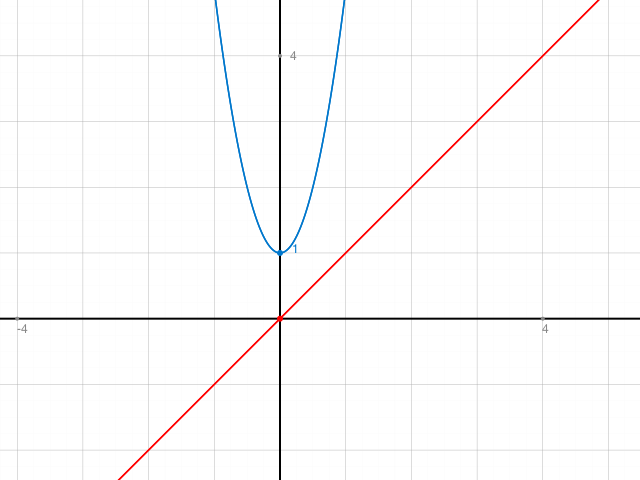
Wenn du diese Funktion anschaust, siehst du, dass sie nicht in ganz IR umkehrbar ist.
Man kommt nämlich wegen ihrer Symmetrie nicht eindeutig von den y-Werten zurück zum x-Wert. Man kann nur einen Ast der Parabel oder den andern verwenden. Das ergibt sich auch aus der Rechnung, die nun folgt.
f(x)= 4x^2+1
Du musst hier f(x) = y einsetzen
y=4x^2+1
und jetzt diese Gleichung Schritt für Schritt nach x auflösen. Zum Schluss x und y vertauschen.
y=4x^2+1 |-1
y - 1 = 4 x^2 |:4
(y-1)/4 = x^2 |±√
Ab hier muss man jetzt wissen, ob man die Umkehrfunktion für den rechten oder den linken Ast der Parabel braucht.
Rechts ist x>0, links ist x<0.
√((y-1)/4) = x oder -√((y-1)/4) = x
x =√((y-1)/4) oder x= -√((y-1)/4)
Aus 4 im Nenner kann man noch die Wurzel ziehen. Somit steht nur noch der Zähler unter der Wurzel
x =√(y-1) / 2 oder x= -√(y-1) / 2
Jetzt x und y vertauschen
y =√(x-1) / 2 oder y= -√(x-1) / 2
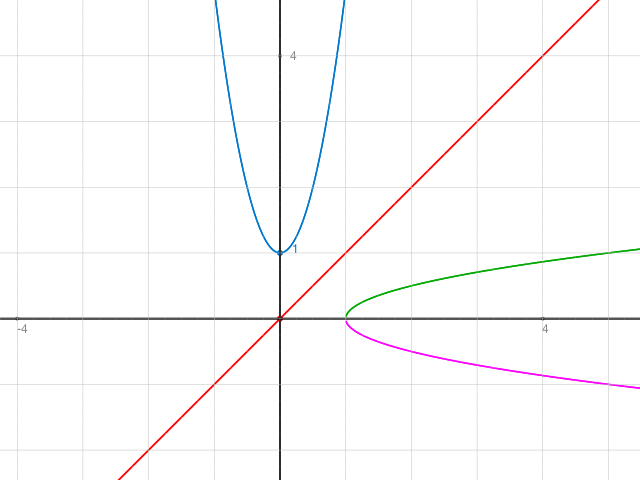
Kontrolle Graph.
Der rechte Ast an y=x gespiegelt ergibt die grüne Umkehrfunktion. Der linke Ast die violette Umkehrfunktion. Beide sind für x≥1 definiert.