Es hilft auch oft, wenn du versuchst, dir mathematische Aussagen, wenn möglich, mal zu veranschaulichen.
Stelle dir so eine \( \epsilon \)-Umgebung mal auf einer Zahlengeraden vor:
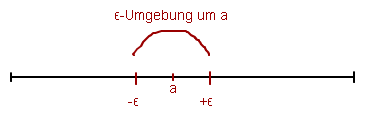
a ist nun der Grenzwert deiner Folge. a ist umgeben von \( -\epsilon \) und \( +\epsilon \).
Ganz wichtig ist, dass \( \epsilon \) hier keine bestimmte Zahl ist. Es ist einfach \( \epsilon > 0 \), was bedeutet, dass \( \epsilon = 1324324543543566 \) oder \( \epsilon = 0,0000000000000000000001 \) sein kann. Es darf nur nicht 0 oder negativ sein.
Jetzt die Definition:
" Eine Folge konvergiert genau dann, wenn in jeder ε -Umgebung um den Grenzwert fast alle (bis auf endlich viele Ausnahmen) Folgenglieder liegen."
Das sieht dann in etwa so aus ( die grünen Punkte sind die Werte der Folgenglieder ):
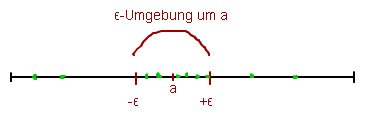
Wenn du die roten Striche bei \(-\epsilon \) und \( +\epsilon \) jetzt immer weiter zusammenziehst, immer näher an das a heran (d.h. Epsilon immer kleiner machst) dann muss immernoch gelten, dass nur endlich viele Punkte ausserhalb dieser Umgebung liegen und der riesige Rest innerhalb. Das kommt doch dem intuitiven Verständnis des Grenzwertes ziemlich nahe, oder?
Jetzt überlege mal in deinem Fall, wieviele Punkte liegen außerhalb einer \( \epsilon \)-Umgebung um einen beliebigen Punkt a? Wenn du z.B. a = 5 wählst, liegen unendlich viele 0-en und 2-en außerhalb. Das kann also nicht der Grenzwert sein. Wenn man a = 2 wählt, liegen unendlich viele 0-en außerhalb. Das kann also auch nicht der Grenzwert sein. Wenn man a = 0 wählt, liegen unendlich viele 2-en außerhalb. Das kann auch nicht der Grenzwert sein. Schlussendlich kannst du eben keinen Punkt in einer beliebig kleinen Epsilon-Umgebung wählen, so dass immer nur endlich viele Folgenglieder außerhalb liegen, weil die Folge eben immer zwischen 0 und 2 wechselt.
Also besitzt sie nach obiger Definition keinen Grenzwert.