Offensichtlich sind dort keine rechten winkel.
Miss mal die folgenden Strecken a, b, c und d. Und die entstehenden Winkel.
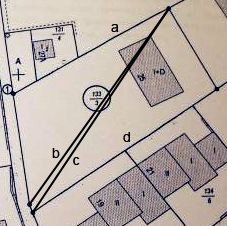
Achtung: d ist hier verkehrt eingezeichnet. d sollte auch am Punkt starten wo auch a b und c starten und geht dann nach rechts unten.
Die Flächen der Dreiecke berechnest du
A1 = 1/2 * a * b * SIN(∠ab)
A2 = 1/2 * b * c * SIN(∠bc)
A3 = 1/2 * c * d * SIN(∠cd)
Addierst du A1 bis A3 erhältst du die Gesamtfläche.