Hi Sommersonne,
ich hab zwar kein Abiturabschluss, sondern nur ein RSA, aber versuchen kann ichs ja mal. Ich mache es aber mit einer einfacheren Funktion, denn deine Funktion kann ich nicht ableiten ^^.
f(x)= e2x-2+2x an der Stelle x0=1
Formel der Taylorentwicklung:
f(x)≈f(x0)+f'(x0)/1!(x-x0)1+f''(x0)/2!(x-x0)2
Nun bildest Du die 2.Ableitungen:
f(x)= e2x-2+2x
f'(x)= 2e2x-2+2
f''(x)= 4e2x-2
jetzt setzt Du dein x0=1 für x in die Ableitungen ein:
f(1)= e2*1-2+2*1= 3
f'(1)= 2e2*1-2+2= 4
f''(1)= 4e2*1-2= 4
f(x)≈ f(1)+f'(1)/1(x-1)+f''(1)/1*2(x-1)2
f(x)≈ 3+4/1(x-1)+4/2(x-1)2 vereinfachen ---> f(x)≈3+4(x-1)+2(x-1)2
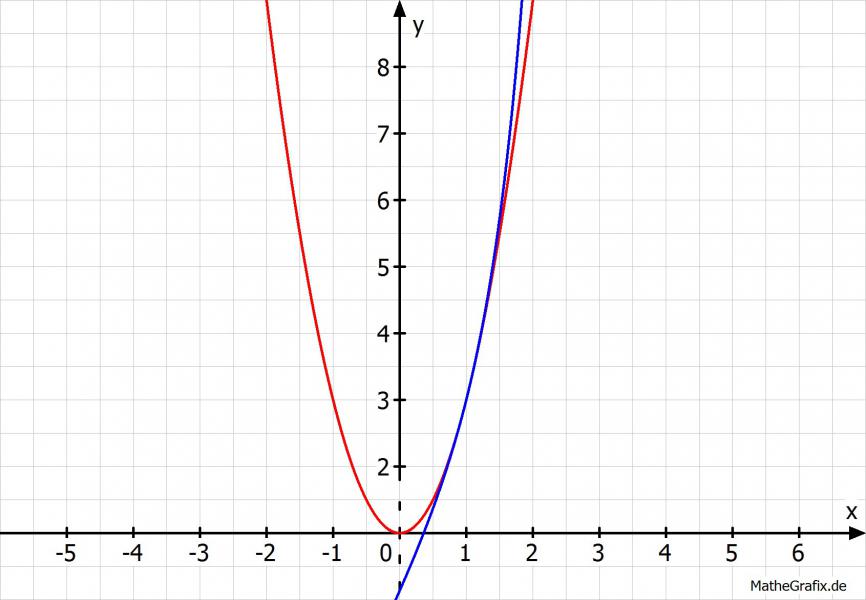
f(x)= e2x-2+2x
f(x)≈3+4(x-1)+2(x-1)2
Mit deiner Funktion konnte ich das nicht, weil ich deine Funktion nicht ableiten konnte ^^.
Grüße