f(x) = e-x * (x3 - 3,5x2 - 6,5x + 9)
Eine Produkt wird dann = 0, wenn zumindest einer der Faktoren = 0 ist.
e-x ≠ 0 für alle x
Also suchen wir die Nullstellen für den Term innerhalb der Klammern.
Durch Raten kommt man auf die 1. Nullstelle x1 = 1
Dann Polynomdivision:
(x3 - 3,5x2 - 6,5x + 9) : (x - 1) = x2 - 2,5x - 9
x3 - x2
---------
-2,5x2 - 6,5x
-2,5x2 + 2,5x
-------------------
-9x + 9
-9x + 9
-----------
0
Die Nullstellen des Terms
x2 - 2,5x - 9
findet man mit der pq-Formel
x2,3 = 1,25 ± √(1,5625 + 9) = 1,25 ± 3,25
x2 = 4,5
x3 = -2
Mit Hilfe der fett angegebenen Nullstellen kann man jetzt eine faktorisierte Form der Funktion angeben:
f(x) = e-x * (x - 1) * (x + 2) * (x - 4,5)
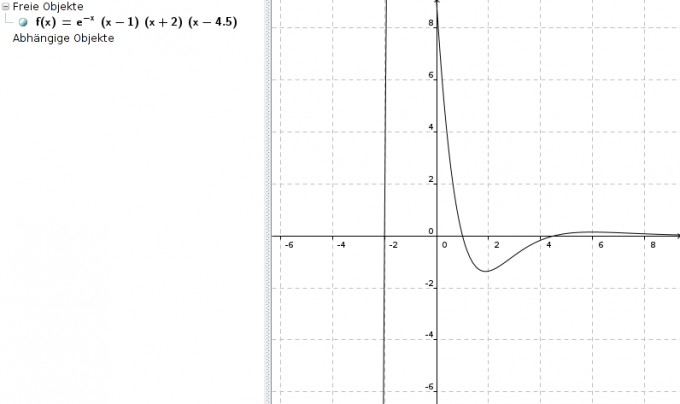
Besten Gruß