Extremwertaufgabe Rechteck

Question

Gegeben ist eine Funktion f(x) mit f(x)=6-0,25x^2  zwischen Kurve und x-Achse ist ein Rechteck einzubeschreiben mit

a) maximalen Umfang

b) maximaler Fläche

Hier soll der maximale Umfang bzw. die maximale Fläche berechnet werden.

Kann mir jemand bitte alles Schritt für Schritt erklären

Answer 1

so in etwa sieht die Problemstellung in einer Skizze aus:

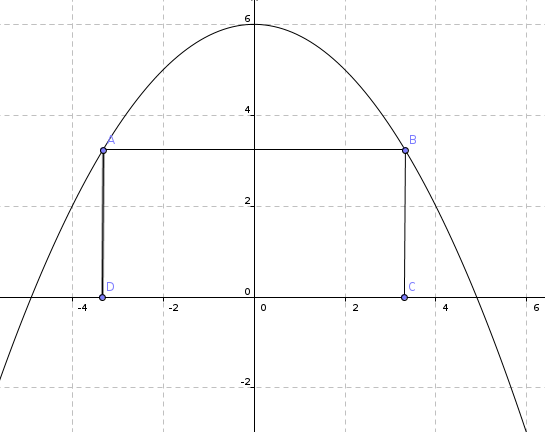
Da das Ganze ja achsensymmetrisch zur y-Achse ist, betrachten wir zunächst nur die rechte Seite.

Der Umfang des gesuchten (halben) Rechtecks (ohne die y-Achse) ist dann, wenn wir den Punkt C in der Skizze mit x bezeichnen:
U(x) = 2x + (6 - 0,25x²) = -0,25x² + 2x + 6
Davon die 1. Ableitung bilden, = 0 setzen, in der 2. Ableitung überprüfen, ob sie für dieses x > 0 ist (Minimum an der Stelle x) oder < 0 ist (Maximum an der Stelle x).

Die Fläche des gesuchten (halben) Rechtecks ist, wenn wir wieder den Punkt C in der Skizze mit x bezeichnen:
A(x) = x * (6 - 0,25x²) = -0,25x³ + 6x
Auch hier 1. Ableitung = 0 setzen, und für die sich ergebenden x-Werte die 2. Ableitung überprüfen.

Bitte versuch das mal selbst; Deine Lösung wird gerne kontrolliert :-)

Besten Gruß 

Comments

Du hast wirklich immer super Antworten (Sowohl erklärend als auch visuell dargestellt!), mein Lob Bruce :-)

---

Vielen Dank für das Kompliment Florean!

Ich brauche die Skizzen immer selbst, weil ich mir sonst gar nicht vorstellen kann, worum es geht :-D

Answer 2

b) Fläche musst du ertsmal Flächeninhalt also A=a*b also EB

und dann musst du herausfinden wie lang a ist und b ,dafür brauchst du eine Skizze der Funktion hier ist das wohl a=2x musst du nachgucken und b=f(x) b ist immer f(x)!!!wenn du einen hast liegt von der funktion ab

und dann musst du A(x) berechnen das ist hier A(x)=2x(6-0,25x²) dann folgt eine notwendige Bedingung also A´(x)=0

damit du die Nullstellen hast und dann die hinreischende Bedingung.

ich hoffe du hast es verstanden wenn nicht schreib mir einfach

das selbe gilt für a) nur mit dem Umfang