Gemeinsamer Punkt aller Kurven der Schar bestimmen

Question

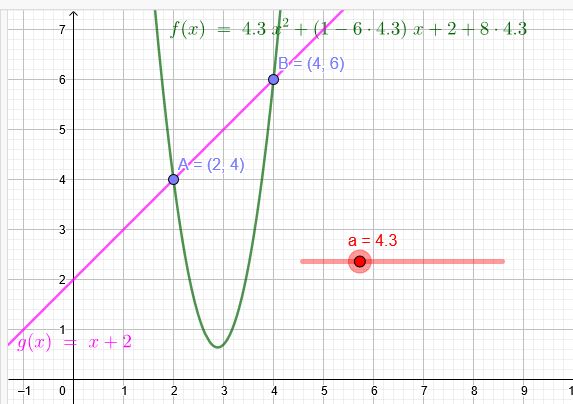
Für jede Zahl a>0 ist eine Funktion f_a(x)= ax²+(1-6a)x+2+8a  . Untersuchen sie rechnerisch ob es Punkte gibt, durch die alle Kurven der Schar gehen.

Answer 1

fa(x) = fb(x)

a·x^2 + (1 - 6·a)·x + 2 + 8·a = b·x^2 + (1 - 6·b)·x + 2 + 8·b

Nun das ganze nach x auflösen:

x = 4 ∨ x = 2

Durch die Stellen 2 und 4 sollten alle Funktionen gehen.

Answer 2

f_a(x)= ax²+(1-6a)x+2+8a
Für einen Schnittpunkt gilt
f_a1 ( x ) = f_a2 ( x )
a1 * x²+ ( 1- 6a1 ) * x + 2 + 8a1 = a2 * x²+ ( 1- 6a2 ) * x + 2 + 8a2
umstellen nach x
a1 * x² - a2 * x^2   +  ( 1- 6a1 ) * x - ( 1- 6a2 ) * x  =  8a2 - 8a1
( a1 - a2 ) * x^2 + ( 1 - 6a1 - 1 + 6a2 ) * x = 8 * ( a2 - a1 )
( a1 - a2 ) * x^2 + ( - 6a1 + 6a2 ) * x = 8 * ( a2 - a1 )
( a1 - a2 ) * x^2 - 6 *  ( a1 - a2 ) * x = -8 * ( a1 - a2 )  | : ( a2 - a1 )
x^2 - 6x = -8
( x - 3)^2 = 1
x- 3 = ±1
x = 4
x = 2