Hi,
es ist zwar schon etwas her, aber ist auch mal eine gute Übung für mich^^
$$ \sum _{k=0}^{\infty}{\frac { 1 }{ \sqrt { (k+1)^3 } }} $$
$$ \lim_{z\to∞} \int_{0}^{∞}\frac { 1 }{ (x+1){ }^{ \frac { 3 }{ 2 } } }dx=[\frac { -2 }{ \sqrt {( x +1)} } ]_0^z= 0-(-2)= 2$$
Durch das negative Vorziechen vor der Klammer, ändert sich das Vorzeichen in der Klammer zu einem Plus
Nochmal in Schritten:
Beispiel diese Funktion
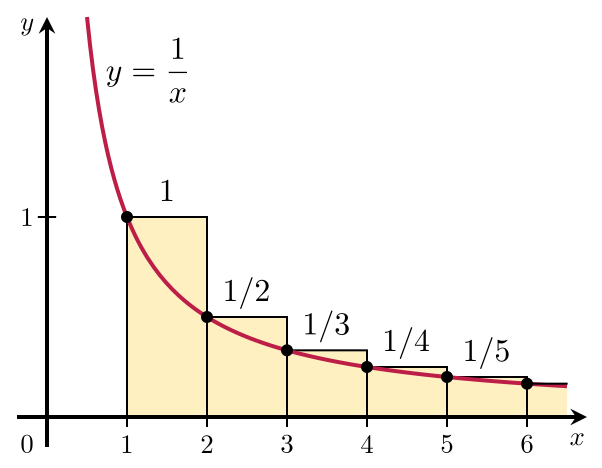
Die Reihe von dieser Funktion wäre ja zum Beispiel $$ \sum _{n=0}^{\infty}{\frac { 1 }{ n }} $$
Und dann könntest Du das als ein uneigentliches Integral aufschreiben und dann schauen, ob der Grenzwert existiert oder bzw. nicht existiert. Wenn der Grenzwert existiert, so ist die Reihe konvergent und wenn sie nicht existiert, dann ist die Reihe divergent.. ich denke Du weißt, wie man ein Uneigentliches Integral berechnet?
Ich hoffe ich konnte Dir ein bisschen helfen.
Falls ich Fehler bei der Rechnung gemacht habe, oder schreibfehler habe, dann bitte kommentieren und verbessern. Wie gesagt ich gehe noch in die Schule und bin kein Student^^