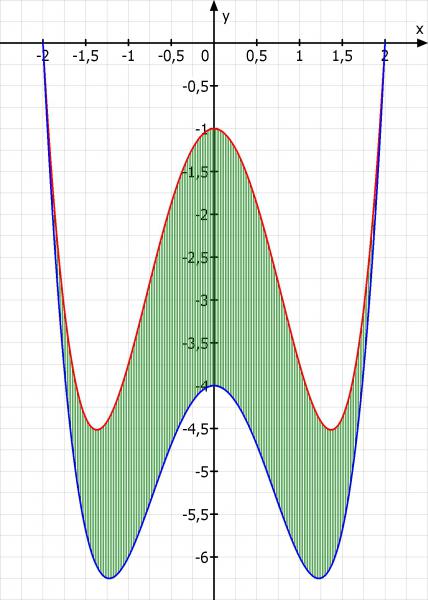
g(x)=x4-3,75x2-1
h(x)=x4-3x2-4
(1) Zeigen Sie, dass das Logo eine achsensymmetrische Figur ist.
Beide Funktionen sind achsensymmetrisch, da in ihnen nur gerade Exponenten vorhanden sind. Damit ist das Logo achsensymmetrisch.
(2) Geben Sie die maximale Breite des Logos an.
g(x) = h(x)
x4 - 3,75x2 - 1 = x4 - 3x2 - 4
-3/4x^2 = -3
x = ±2
Die maximale Breite ist damit 4 cm.
(3) Die Punkte P und Q liegen zwei Millimeter direkt "unter" den tiefsten Punkten der oberen Begrenzungslinie des Logos. Zur Befestigung verbindet eine Querstrebe die Punkte P und Q. Bestimmen Sie rechnerisch die Länge der Querstrebe.
Extremstellen von g. g '(x) = 0
g'(x) = 4·x^3 - 7.5·x = x·(4·x^2 - 7.5)
Eine Nullstelle ist bei 0 (Maximum)
4·x^2 - 7.5 = 0
x = √30/4
Die Länge ist also 2 * √30/4 = √30/2 = 2.739 cm
(4) Die Graphen von g und h besitzen jeweils genau zwei Wendepunkte. Weisen Sie rechnerisch nach, dass die Wendepunkte der Graphen der Begrenzungskurven des Logos an verschiedenen Stellen liegen.
Wendestellen von g. g''(x) = 0
g''(x) = 12·x^2 - 15/2 = 0
x = √10/4
Wendestellen von h(x). h''(x) = 0
h''(x) = 12·x^2 - 6 = 0
x = √2/2
Damit sind die Stellen verschieden.
Skizze: