Kostenfunktion. Bestimmen Sie die minimal möglichen Kosten

Question

Gegeben sei die folgende Kostenfunktion:

K(x) = 1/3*x³ - 3/2 *x² + 6,5

Bestimmen Sie die minimal möglichen Kosten.

Danke dir, euch!

Answer 1

K(x) = 1/3*x³ - 3/2 *x² + 6,5

Für ein Extremum, in diesem Falle also ein Minimum, setzen wir die 1. Ableitung = 0:

K'(x) = x² - 3x

x² - 3x = 0 | + 3x

x² = 3x | : x

x = 3

Wir bilden die 2. Ableitung, um zu sehen, ob an der Stelle x = 3 ein Minimum oder Maximum vorliegt:

K''(x) = 2x - 3

K''(3) = 2 * 3 - 3 = 3 > 0 | Also liegt an der Stelle x = 3 ein Minimum vor.

Die Kosten betragen dann

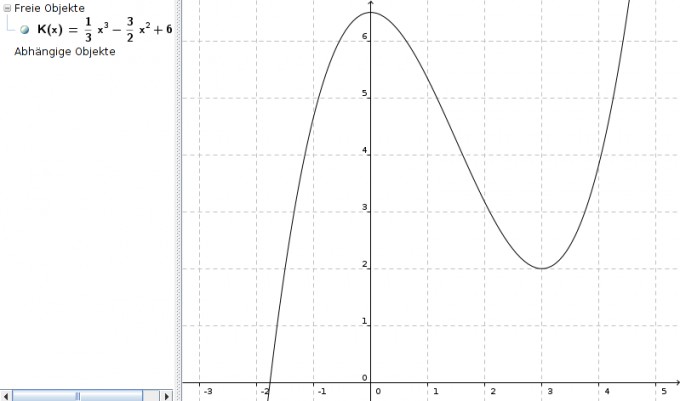
K(3) = 1/3 * 3³ - 3/2 * 3² + 6,5 = 9 - 13,5 + 6,5 = 2

wie auch folgende Graphik recht gut verdeutlicht:

Besten Gruß

Comments

Mir bleibt die Spucke weg! Ein weiteres mal vielen Dank an dich!

---

Sehr gern geschehen!

Danke für den Stern :-D

---

Brucybabe du kannst so schön erklären!!!

plusspunkt von mirrrrr :)

---

Auch an Dich herzlichen Dankkkk, mein lieber Emre :-)

---

Haha immerrr und immerrr wieder gerneee :) :)

---

Du hast durch das Dividieren durch x eine Nullstelle der ersten Ableitung verloren. x=0 ist auch eine Nullstelle.

Besser wäre:
\(x^2-3x=0\Rightarrow x(x-3)=0\)
Und jetzt verwenden, dass ein Produkt genau dann Null ist, wenn einer der Faktoren Null ist. Damit erhältst du dann beide Nullstellen.

---

sorry, das ich blöd fragen muss, aber kommt da nicht bei der 1. Ableitung K´(x)= 3x² - 2x raus?

---

@ 10001000Nick1:

Damit hast Du natürlich Recht - danke für den Hinweis!

Zum Glück wirkt sich das letztlich auf die Lösung nicht aus, weil an der Stelle x = 0 ja ein lokales Maximum vorliegt.

Mathematisch korrekt wäre in der Tat Dein Vorgehen gewesen.

---

ich hoffe keiner sieht meine blöde frage... weil löschen kann ich die nicht... vergesst es... sorry :)

---

@ Gast:

K(x) = 1/3*x³ - 3/2 *x² + 6,5

Wir bilden die 1. Ableitung, indem wir den jeweiligen Exponenten mit dem "Vorfaktor" multiplizieren und dann den Exponenten um 1 verringern, also (die Konstante +6,5 fällt bei der Ableitung weg, weil sie nur eine Verschiebung des Graphen um 6,5 nach sich zieht, sich aber nicht auf die Steigung auswirkt):

K'(x) = 3 * 1/3 * x^3-1 - 2 * 3/2 * x^2-1 = 1 * x² - 3 * x¹ = x² - 3x

Besten Gruß

---

aaa... du hast es doch gesehen... wie peinlich :)

nachgerechnet, verstanden und abgehakt. ;)

---

Jeder macht Fehler ...

ich auch, wie Du an dem Kommentar von 10001000Nick1 siehst :-)