Rekonstruktion von Funktionen benötige Hilfe & Tipps

Question

Eine ganzrationale Funktion drittem Grades ist symmetrisch zum Koordinatenursprung und hat ein Tiefpunkt bei T(1/-2).

Wie lautet die Funktionsgleichung?

Answer 1

f ( x ) = a*x3 + b * x
f´( x ) = 3*a*x^2 + b;

f ( 1 ) = a + b = -2
f ´( 1 ) = 3a + b = 0
2a = 2
a = 1
b = -3
f ( x ) = x^3 - 3*x
Probe
f ( 1 ) = 1 - 3 = -2
f ´( 1 ) = 3 - 3 = 0
f ´´ ( x ) = 6 * a * x
f ´´ ( 1 ) = 6  = Tiefpunkt

Answer 2

Funktion 3. Grades allgemein:

f(x) = ax³ + bx² + cx + d

f'(x) = 3ax² + 2bx + c

f''(x) = 6ax + 2b

Wir suchen die 4 Unbekannten a, b, c und d.

Symmetrie zum Koordinatenursprung. Das heißt d = 0 und f(-x) = -f(x)

f(-x) = a*(-x)³ + b * (-x)² + c*(-x) + d = -ax³ - bx² - cx - d = -f(x)

b*x² + d = -bx² - d

2bx² = 0

bx² = 0

b = 0

Damit vereinfacht sich die Funktionsgleichung zu

f(x) = ax³ + cx

f'(x) = 3ax + c

Tiefpunkt bei T(1/-2), also

f(1) = -2 | a + c = -2 | a = -2 - c

und

f'(1) = 0 | 3a + c = 0

3 * (-2 - c) + c = 0 | -6 - 2c = 0 | -2c = 6 | c = -3

a = -2 - c = -2 + 3 = 1

f(x) = x³ - 3x

 

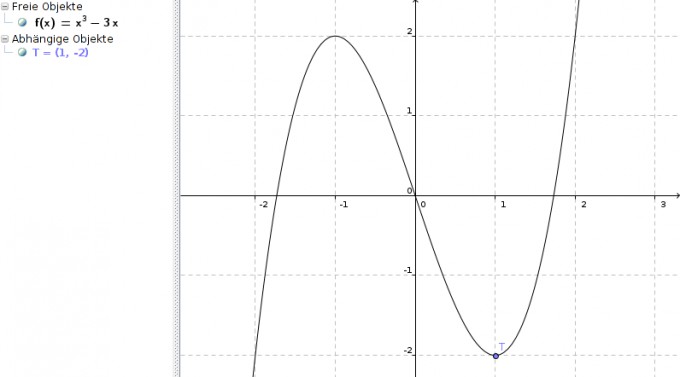
Besten Gruß