Komplexe Übungen - Exponentialfunktionen:
Gegeben ist die Funktionenschar \( f_{k} \) durch die Gleichung \( f_{i}(x)=2 k x^{2} e^{k-1} \) mit \( k>0 \). Ihre Graphen seien \( G_{i} \).
a) Bestimmen Sie das Verhalten der Graphen \( G_{2} \) im Unendlichen und ermitteln Sie die Gleichung der Asymptote.
Untersuchen Sie die Graphen \( G_{i} \) auf Schnittpunkte mit den Koordinatenachsen.
Extrem- sowie Wendepunkte und berechnen Sie deren Koordinaten.
(Graphen von \( G_{1} \) und der ersten Ableitung von \( f_{1} \) - siehe Abbildung)
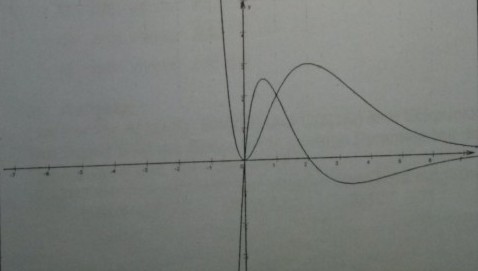
b) Eine Gerade \( x=u \) mit \( u>\frac{1}{2} \) schneidet \( G_{i} \) im Punkt \( P \) und den Graphen der zweiten Ableitung von \( f_{k} \) im Punkt \( Q \). Für welches \( u \) wird die Strecke \( \overline{P Q} \) maximal?
c) \( G_{1} \) und der Graph der ersten Ableitung von \( f_{1} \) begrenzen eine Fläche vollständig. Berechnen Sie die Maßzahl des Flächeninhaltes dieser Fläche.
d) Die Fläche, die durch den Graph der ersten Ableitung von \( f_{1} \) und die \( x \) - Achse vollständig begrenzt wird, rotiert um die x-Achse. Ermitteln Sie das Volumen des Rotationskörpers.
e) Die Ursprungsgerade, welche Tangente an \( G_{1} \) ist, sei \( t_{1} \) und ihr Berührpunkt sei \( R \). Zeigen Sie, dass \( R \) ein Punkt des Graphen der ersten Ableitung von \( f_{1} \) ist und ermitteln Sie eine Gleichung für den Parameter \( k \) so, dass die Tangente \( t_{2} \) im Punkt \( R \) an den Graphen der ersten Ableitung von \( f_{t} \) senkrecht zu \( t_{1} \) verläuft.