Kurvendiskussion komplexe Aufgabe mit Tangenten

Question

Komplexe Übungen - Exponentialfunktionen:

Gegeben ist die Funktionenschar $f_{k}$ durch die Gleichung $f_{i}(x)=2 k x^{2} e^{k-1}$ mit $k>0$. Ihre Graphen seien $G_{i}$.

a) Bestimmen Sie das Verhalten der Graphen $G_{2}$ im Unendlichen und ermitteln Sie die Gleichung der Asymptote.
Untersuchen Sie die Graphen $G_{i}$ auf Schnittpunkte mit den Koordinatenachsen.

Extrem- sowie Wendepunkte und berechnen Sie deren Koordinaten.

(Graphen von $G_{1}$ und der ersten Ableitung von $f_{1}$ - siehe Abbildung)

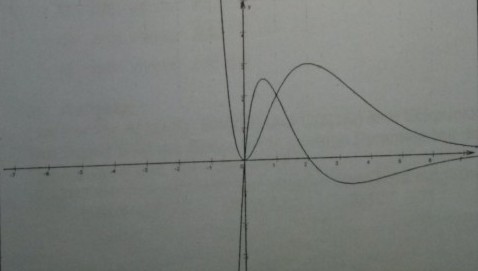
b) Eine Gerade $x=u$ mit $u>\frac{1}{2}$ schneidet $G_{i}$ im Punkt $P$ und den Graphen der zweiten Ableitung von $f_{k}$ im Punkt $Q$. Für welches $u$ wird die Strecke $\overline{P Q}$ maximal?

c) $G_{1}$ und der Graph der ersten Ableitung von $f_{1}$ begrenzen eine Fläche vollständig. Berechnen Sie die Maßzahl des Flächeninhaltes dieser Fläche.

d) Die Fläche, die durch den Graph der ersten Ableitung von $f_{1}$ und die $x$ - Achse vollständig begrenzt wird, rotiert um die x-Achse. Ermitteln Sie das Volumen des Rotationskörpers.

e) Die Ursprungsgerade, welche Tangente an $G_{1}$ ist, sei $t_{1}$ und ihr Berührpunkt sei $R$. Zeigen Sie, dass $R$ ein Punkt des Graphen der ersten Ableitung von $f_{1}$ ist und ermitteln Sie eine Gleichung für den Parameter $k$ so, dass die Tangente $t_{2}$ im Punkt $R$ an den Graphen der ersten Ableitung von $f_{t}$ senkrecht zu $t_{1}$ verläuft.

Answer 1

Dein Foto ist leider nicht immer zu entziffern.

f ( x ) = 2 * k * x² * e^k-x ???

Desweiteren habe ich die 1.Ableitung  f ´( x ).
k ist noch unbestimmt.

Desweiteren eine Gerade die durch den Ursprung geht  und
Tangente an f ( x ) ist. [ Aber nicht im Punkt ( 0 | 0 ) ].

Also Steigung der Geraden = Steigung im Punkt  R
f ( x ) = m * x
und
f ´( x ) = m

???

Das könnte der erste Schritt zur Lösung sein.

Comments

ich versteh leider immer noch nicht ganz wie man da weiter soll

also die Tangente geht nicht durch den punkt 0/0

aber das wird doch beschrieben mit (durch den Koordinatenursprung ) 

---

ich brauche die richtige Orginalgleichung der Funktion und ich
brauche den von e.) in leserlicher Form.

---

Gegeben ist die Funktionenschar fk durch die Gleichung fk(x)=2*k*x²*e^k-x mit k größer 0.Ihre Graphen seien Gk.

Aufgabe: Die Ursprungsgerade ,welche Tangente an Gk ist,sei t1 und Ihr Berührpunkt sei R.Zeigen Sie ,dass R ein Punkt des Graphen der ersten Ableitung von fk ist und ermitteln Sie eine Gleichung für den Parameter k so,dass die Tangente t2 im Punkt R an den Graphen der ersten Ableitung von fk senkrecht zu t1 verläuft.

---

Hier schon einmal eine erste Antwort

---

t1 = 2 * k * e^k-1 * x
m1 = 2 * k * e^k-1

f ´´ ( x ) = 2 * k * e^k-1 * ( x² - 4 * x + 2 )
Steigung in R
f ´´ ( 1 ) = 2 * k * e^k-1 * ( 1 - 4 + 2 )
f ´´ ( 1 ) = -2 * k * e^k-1
m2 = -2 * k * e^k-1

Orthogonal zueinander
m1 = - 1 / m2
2 * k * e^k-1  = - 1 /  ( -2 * k * e^k-1 )
4 * k² * e^2k-2 = 1
k = 0.685

Leider kommt hier kein schönes Ergebnis heraus.

Vieleicht hilft dir die Berechnung doch weiter.