Aufgabe 6:
Finde den fehlenden x- bzw. y-Wert, sodass das Wertepaar eine Lösung der linearen Gleichung \( 5 x+2 y=10 \) ergibt:
a) \( (1 \mid \square) \)
b) \( (\square | 5) \)
c) \( (4 \mid \square) \)
d) \( (\square \mid -10) \)
e) \( (-1 \mid \square) \)
f) \( (\square \mid -0,5) \)
Aufgabe 7:
Jede Gerade stellt die Menge der Lösungen einer Gleichung dar. Welche der Gleichungen passt zu welcher Geraden? Zu einer Geraden können mehrere der Gleichungen passen.
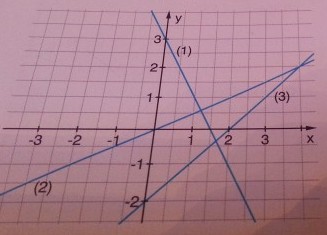
a) \( 4 x+2 y=6 \)
b) \( 5 y-5 x=-10 \)
c) \( 2 y-x=0 \)
d) \( y=3-2 x \)
e) \( 12 x+6 y=18 \)
f) \( y=-2+x \)