Aufgabe Turm:
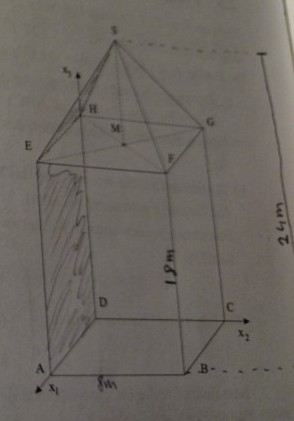
Ein Turm hat die Form einer senkrechten quadratischen Säule, der eine senkrechte Pyramide aufgesetzt ist (siehe Skizze).
Die Gesamthöhe des Turms beträgt \( 24 \mathrm{~m} \), die horizontalen Kanten sind \( 8 \mathrm{~m} \), die vertikalen Kanten sind \( 18 \mathrm{~m} \) lang. Der Punkt D liegt im Ursprung eines kartesischen Koordinatensystems mit der Längeneinheit \( 1 \mathrm{~m} \).
a) Geben Sie die Koordinaten aller Punkte an und berechnen Sie den Neigungswinkel des Daches (Winkel zwischen Pyramidengrundfläche und Seitenfläche) sowie die Größe der Dachfläche.
b) Im Punkt \( \mathrm{P}(18|4| 0) \) steht ein \( 8 \mathrm{~m} \) hoher Fahnenmast. Berechnen Sie die Länge des Schattens auf Boden und Turmwand, wenn …
Ich habe eine Verständnisfrage zur Aufgabe a):
Der erste Teil der Aufgabe war kein Problem, daher hier einmal die Auflistung der Punkte und deren Koordinaten:
A(8|0|0|), B(8|8|0|), C(0|8|0|), D(0|0|0|), E(8|0|18), F(8|8|18), G(0|8|18), H(0|0|18), S(4|4|24), M(4|4|18)
Nun wollte ich die Aufgabe mit dem Neigungswinkel auf folgende Art lösen:
Eine Ebene auis den Punkten E,H,S bilden. Eine weitere Ebene aus den Punkten A,D,E,H.
Dann mittels Kreuzprodukt aus den beiden Richtungsvektoren jeweils die Normalenvektoren ermitteln und mit der Formel für die Bestimmung des Winekls zwischen 2 Ebenen dann den Neigungswinkel berechnen.
(cos a = n1*n2 / |n1|*|n2|)
Gesagt getan, Ergebnis 0. Was habe ich falsch gemacht?
Und noch eine weitere Frage: Wie berechnet man die Dreiecksfläche?