Polynomfunktionen 2.Ordnung rotiert um die y-Achse. Volumen der Glaskuppel?

Question

Eine Glaskuppel wird von zwei Polynomfunktionen 2.Ordnung begrenzt, die um die y- Achse rotieren. Die erste hat ihren Extremwert in (0/1) und ihre Nullstellen in (-0,5/0) und (0,5/0). Die zweite hat ihren Extremwert in (0/0,5) und ihre Nullstellen in (-1/0) und (1/0).
Fertigen sie eine Skizze an und berechnen sie das Volumen der Kuppel!

Meine Ideen:
Mein Ansatz wäre mal bei f (x) ax^{2}+bx+c=0 für eine Polynomfunktion 2.Ordnung. Aber dann?

Vielen Dank

Comments

Hier bekommst du bereits Hilfe. Doppelposts sind nicht gern gesehen.

---

Ich habe diese Frage nur einmal auf dieser Seite gepostet und ich habe momentan einen absoluten Hänger!

Answer 1

Die Glaskuppe sollte dann vielleicht so aussehen:

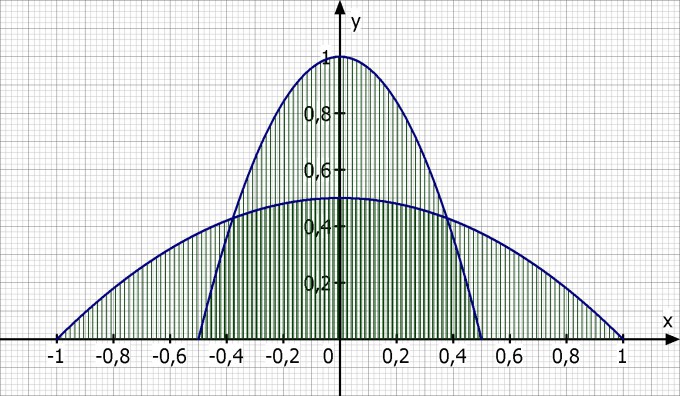
Die Funktionen wären

f(x) = - 1/0.5^2·x^2 + 1 = 1 - 4·x^2

g(x) = - 0.5·x^2 + 0.5 = 0.5 - 0.5·x^2

Ich persönlich finde es einfacher diese um die x-Achse rotieren zu lassen. Dazu müsste man die Umkehrfunktionen bilden. Ich glaube es gab aber auch eine direkte Formel, wenn der Graph um die y-Achse rotiert. Probiere das aber zunächst mal mit der Umkehrfunktion.

Comments

Wahnsinn! Danke.

2 Bitten hätte ich noch: Den Weg mit dem einsetzen in die Funktion.

und bitte Volumsformel um die y-Achse.

danke danke

---

Schau mal bei Wikipedia. Dort findest du die Formel.

https://de.wikipedia.org/wiki/Rotationsk%C3%B6rper#Rotation_um_die_y-Achse

Du solltest zum berechnen der Grenzen noch den Schnittpunkt der Funktionen bestimmen.

---

Die beiden Schnittpunkte ergeben sich ja  aus

1 - 4x² = 0,5 - 0,5 x²

x² - 1/7 = 0 einsetzen in die formel

x₁ = √1/7

x₂ = -√1/7

Volumen für die beiden Kuppeln alleine ist auch verständlich.

Die niedrige hat

 

oder?