Aufgabe Raumgeometrie:
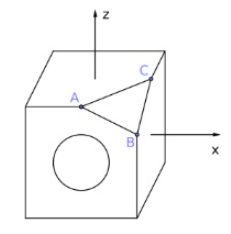
Du siehst hier einen (leeren) Würfel der Kantenlänge 4, dem eine Ecke weggeschnitten wurde. Die Punkte \( A \) und \( C \) waren Mittelpunkte ihrer Kanten, der Punkt \( B \) liegt in der Höhe 3 über dem Boden des Würfels. Der Nullpunkt des vorgegebenen Koordinatensystems liegt im Zentrum des Würfels, und \( B \) ist der Punkt mit den Koordinaten \( (2,-2,1) \).
(a) Die Mittelpunkte der Seitenflächen des Würfels sind die Ecken eines wohlbekannten regelmäßigen Körpers. Zeichne eine Skizze und schreibe seinen Namen dazu.
(b) Berechne die Größe des Winkels \( \beta \) des Dreiecks \( A B C . \)
(c) Bestimme eine Gleichung und eine Parameterdarstellung der Ebene durch \( A, B \) und \( C \).
(d) Im Innern des Würfels befinde sich eine Kugel, die alle sechs Seitenflächen berührt. Wurde die Schale der Kugel beschädigt, als die Ecke des Würfels (durch einen ebenen Schnitt) abgetrennt wurde?
(e) Aus dem Zentrum des Würfels leuchtet ein Zwerg mit einem Laserpointer in der Richtung
\( \vec{v}=\left(\begin{array}{c} 1 \\ -1 \\ 2 \end{array}\right) \)
Verlässt der Strahl das Innere des Würfels durch die (offene) Fläche des Dreiecks \( A B C ? \) Beschreibe einen Weg, dies zu entscheiden.
(f) Auf der dir zugewandten Seitenfläche des Würfels siehst du einen Kreis um den Flächenmittelpunkt mit dem Radius \( 1 . \) Notiere eine Parameterdarstellung für den Ortsvektor \( \vec{x}(t) \) des allgemeinen Punktes der Kreislinie und gib Auskunft, welches geometrische Gebilde entsteht, wenn du alle Vielfachen \( s \vec{x}(t) \) mit \( s \geq 0 \) für alle diese \( \vec{x}(t) \) bildest. [Hinweis: Dazu musst du nichts rechnen.]
(g) Einfallender Lichtstrahl, Lot und reflektierter Strahl liegen in einer Ebene, hast du mal im Physikunterricht gelernt. Stelle dir vor, ein Lichtstrahl mit dem Richtungsvektor \( -\vec{v} \) treffe im Mittelpunkt des Deckels des Würfels auf, da, wo in der Abbildung die \( z \)-Achse aus dem Deckel kommt. Das Lot ist natürlich eine Flächennormale. Gib die Ebene an, von der in der Aussage die Rede ist, und gib eine Darstellung des reflektierten Strahls in der üblichen Weise.
Problem:
Wie bekomme ich hier die Koordinaten für A und C raus? Und was genau muss ich für Raumgeometrie können?