Aufgabe:
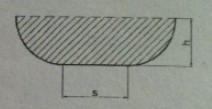
Der Querschnitt des abgebildeten, oben offenen Kanals ist begrenzt durch zwei Viertelkreisbögen und durch eine Strecke der Länge \( s \geq 0 . \) Die Höhe des Kanals ist \( h \).
Berechnen Sie den Inhalt der schraffierten Querschnittsfläche \( A(h) \) in Abhängigkeit von der Höhe h, wenn der Umfang (2 Viertelkreisbögen und Strecke s) 5 LE beträgt.
Bestimmen Sie h so, dass die Querschnittsfläche A den größten Wert besitzt. Berechnen Sie diesen Wert. (Teilergebnis: \( \left.A(h)=5 h-\frac{1}{2} h^{2} \pi\right) \)
Ansatz:
Auf die von h abhängige Flächenformel bin ich gekommen. Ich habe dafür mit folgender Nebenbedingung gerechnet:
5 = hπ+s
s = 5-hπ
A'(h) = 5-hπ
h = 5/π
Das in die zweite Ableitung, und ich erhalte ein Maximum, also das passt das ja. Setze ich 5/π für h jedoch in die Nebenbedingung für s ein, erhalte ich für s 0. Kann das sein?