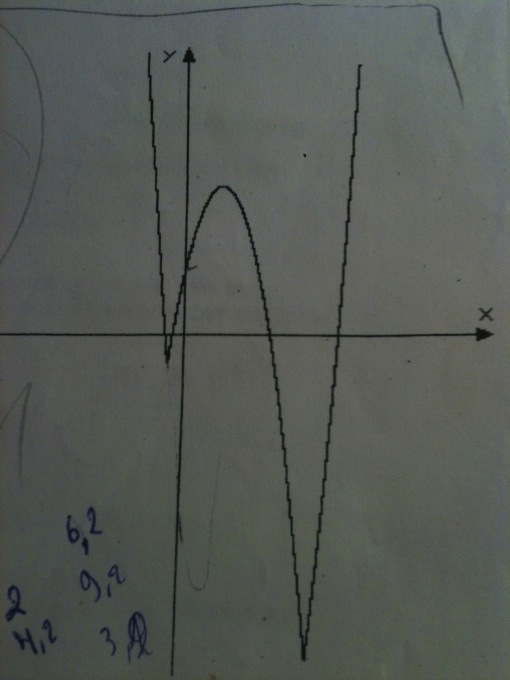
Gegeben:
\( f: I R \rightarrow I R, \quad f(x)=\left|-2 x^{2}+7 x+4\right|-2 x-2 \) (siehe Abbildung)
I) Zerlegen Sie IR in möglichst wenige Intervalle \( \left(I_{k}\right) \), auf denen \( \mathrm{f} \) injektiv ist.
II) Geben Sie für eines der Intervalle aus I) die Umkehrfunktion \( \mathrm{f}^{*} \) von \( \mathrm{f}: \mathrm{I}_{\mathrm{k}} \rightarrow \mathrm{f}\left(\mathrm{I}_{\mathrm{k}}\right) \) an und skizzieren Sie den zugehörigen Graphen in nebenstehendes Koordinatensystem.