a,b und c bei einer Parabel bestimmen! (Kurze Aufgabe)

Question

Hallo erstmals.

Ich habe folgende Werte gegeben: Die Parabel schneidet die y-Achse bei P (0/-8) und hat ihren Scheitelpunkt bei in S (-3/ 5) .

Ich habe folgendes gemacht: -8 = (x+3)²+5 = x² +6x +22

Das stimmt aber glaube ich nicht, da ich ja auch a rausbekommen muss. Ich bin einfach davon ausgegangen das das eine Normalparabel ist. Wie ist das richtig?

LG

Answer 1

Hi,

der Anfang war gut. Einsetzen in die Scheitelpunktform.

y = a(x+3)^2 + 5

Nun P einsetzen:

-8 = a(0+3)^2 + 5  |-5

-13 = 9a

a = -13/9

--> f(x) = -13/9(x+3)^2 + 5

Das noch in die allgemeine Form überführen (ausmultiplizieren) ;).

f(x) = -13/9*x^2 - 26/3*x - 8

Grüße

Comments

Dankeschön :) Mein Gedanke war ja schon mal richtig :D

---

Yep war er! :)

Gerne

Answer 2

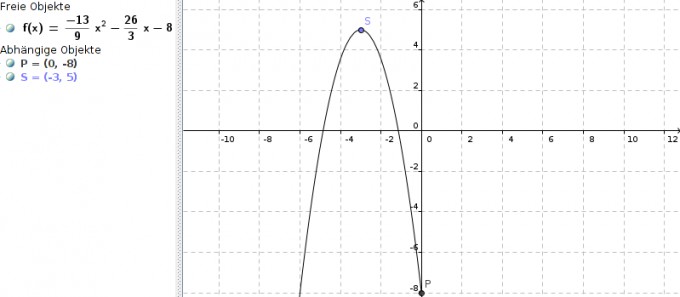
allgemeine Form einer Parabel:

f(x) = ax² + bx + c

Wir haben gegeben:

f(0) = a * 0² + b * 0 + c = -8 | also c = -8

I. f(-3) = a * 9 + b * (-3) - 8 = 9a -3b - 8 = 5 | 9a - 3b = 13

Wegen Scheitelpunktes:

f'(x) = 2ax + b

II. f'(-3) = -6a + b = 0

a = -1,44444... = -1 - 4/9 = -9/9 - 4/9 = -13/9

b = -8,66666... = -8 - 2/3 = -24/3 - 2/3 = -26/3

f(x) = -13/9*x² - 26/3*x - 8

Besten Gruß