Analytische Geometrie: Übungen
Eine Lagerhalle hat die viereckige Grundfläche \( A B C D \), die in der \( x-y \) Ebene liegt, und die schräge Dachfläche \( EFGH \). Alle Wände seien natürlich lotrecht. Außerdem soll \( E \) (nicht überraschenderweise) „oberhalb" von \( A \) liegen, \( F \) "oberhalb" von \( B \) usw. (siehe Skizze).
Ergänzen Sie zunächst einmal die Skizze.
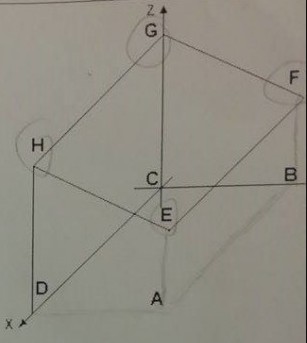
Alle Angaben in Metern.
Es sind gegeben: \( E(20|15| 10) \quad F(0|15| 10) \quad G(0|0| 13) \) und \( H(20|0| 13) \)
Geben Sie die Koordinaten der Punkte \( A, B, C \) und \( D \) an.
Weisen Sie nach, dass die Dachfläche ein Rechteck ist. Vergessen Sie dabei nicht, dass Sie zunächst einmal begründen müssen, dass es sich hier um ein ebenes Viereck handelt.
Berechnen Sie den Diagonalenschnittpunkt der Dachfläche und den Winkel, unter dem sich diese Diagonalen schneiden.
Berechnen Sie die Dachneigung, d.h. den Winkel, den die Dachfläche mit der Horizontalen bildet.
Begründen Sie, dass die Wandflächen \( D A E H \) und \( C B F G \) in zueinander parallelen Ebenen liegen.
Im Punkt \( P(4|5| z) \) soll ein 2 Meter hoher Blitzableiterstab montiert werden, der orthogonal zur Grundfläche steht.
Ansatz/Problem:
Wie kann man denn die Koordinaten bestimmen wenn man keine gleichen Vektoren hat. Ich würde eigentlich sagen das man A ausrechnen kann, indem man A=OE + FB rechnet, aber B hat man ja auch nicht.