Bestimmen Sie die Bereiche, in denen die angegebene Funktion
monoton wachsend und fallend ist:
Du hast versucht einen Extrempunkt zu bestimmen. Dies war jedoch
nicht gefragt. Es gibt auch Funktionen ohne Extrempunkt die unterschiedliche
Monotonie haben. Siehe a.)
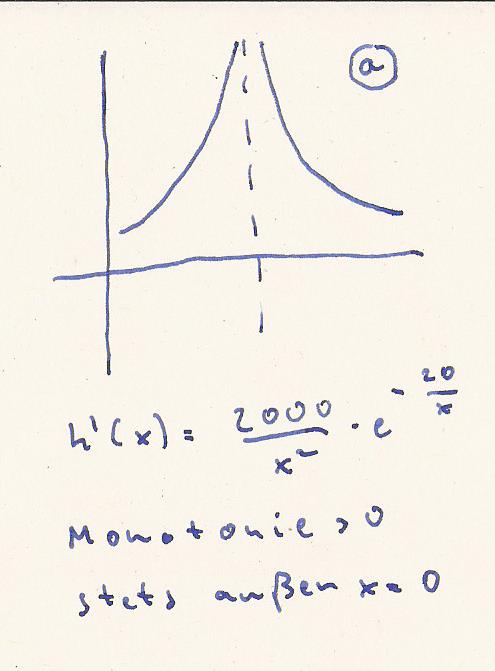
Monoton steigend heißt : 1.Ableitung > 0
Die erste Ableitung ist stets > 0 außer bei x = 0
Die Antwort auf die Fragetsellung wäre.
Die Funktion ist in den Bereichen ] -∞ ; 0 [ und
] 0 ; ∞ [ monoton steigend.
Oben rechts auf dieser Seite ist ein Funktionsplotter.
Dort kannst du dir den genauen Verlauf der Funktion
einmal zeichnen lassen.