Welcher Punkt auf der Hyperbel hat von Q die kleinste Entfernung? (Extremwertaufgabe)

Question

\( y^{2}-x^{2}=1 y>0 Q(1,0) \)
Zielfunktion (enthält den Punkt Q): \( d^{2}=(x-1)^{2}+y^{2} \)
Die Ausgangsfunktion (also die Nebenbedindung) nach \( y^{2}=1+x^{2} \) umgestellt und in die Zielfunktion einsetzen \( d^{2}=(x-1)^{2}+1+x^{2} \) ausmultiplizieren \( d^{2}=2 x^{2}-2 x+2 \)
ableiten \( d^{\prime 2}=4 x-2 \) das muss gleich null sein umstellen nach \( x \) ergibt \( x=1 / 2 \)
in die Nebenbedingung einsetzen \( y=\sqrt{1+\frac{1}{4}} \)
Nochmal ableiten wegen Überprüfung \( d^{\prime \prime 2}=4 \) das ist ungleich Null.

1) Kann mir jemand die 2. Zeile explizit erklären? (Skizze?, irgendwas mit dem Abstand durch Pythagoras?)

2) Desweiteren würde ich gerne verstehen, warum die Funktion d², d² bleiben darf, warum wird sie nicht zu d umgeformt wird, bevor sie abgeleitet wird? (ich weiß, dass das Ergebnis nach dem Auflösen unbeeinflusst bleibt)

Außerdem habe ich allgemein Schwierigkeiten, nachzuvollziehen, wie sich Haupt- und Nebenbedingung zusammensetzen.

Answer 1

Du sollst den Punkt P(x;y) auf der Hyperbel (mit y>0) finden, der von Q(1;0) die kleinste Entfernung hat?

Hast du dir schon mal eine Zeichnung gemacht?

Ja? Dann wähle irgendeinen Beispielpunkt P auf der Hyperbel und verbinde den mit Q.

Jetzt kannst du (mit Pythagoras) den Abstand d von P nach Q berechnen. Es ist ja dann:

d^2 =(x-1)^2+y^2

Und nun hast du zwei Variablen x und y, aber du weisst, dass y^2= 1+x^2

(weil der Punkt P ja auf der Hyperbel herumliegt)

(das wird komischerweise dann als Nebenbedingung verkauft?!)

Setze also einfach ein und du bekommst d^2 (x)= (x-1)^2+ 1 +x^2

und davon suchst du dann die Extrema.

Comments

Damit wurde glaube ich Zielfunktion gemeint.

 d² =(x-1)²+y² 

Ist das die Nebenbedingung?

y²= 1+x² 

Ist das die Hauptbedingung?

Ich habe es skizziert: Das Dreieck in die Skizze.

Aber bei d² =(x-1)²+y²  ist das (x-1) für mich nicht ganz schlüssig.

Answer 2

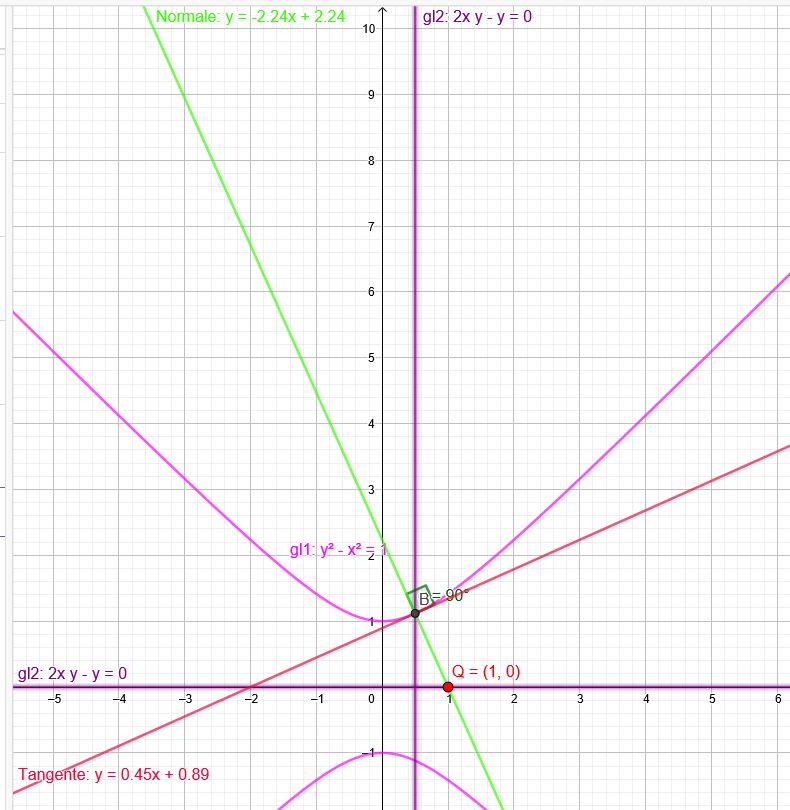
\( y^{2}-x^{2}=1     y≥0      Q(1|0) \)

\(f(x,y)=-x^2+y^{2}-1\)

\(f_x(x,y)=-2x\)

\(f_y(x,y)=2y\)

\(f'(x)=-\frac{f_x(x,y)}{f_y(x,y)}\)  Tangentensteigungen an die Hyperbel

\(f'(x)=-\frac{-2x}{2y}=\frac{x}{y}\)

Die Normalensteigung ist nun  \(n'(x)=-\frac{y}{x}\)

Die Normale geht durch \(Q(1|0) \)

\(\frac{y-0}{x-1} =-\frac{y}{x} \)

\(yx =-yx +y\)

\(2yx-y =0\)

\(y(2x-1) =0\)

\(y=0\)

\(x=0,5\)

Die Gerade  \(x=0,5\) geht durch den Berührpunkt auf der Hyperbel  \( y^{2}-x^{2}=1 \) :

\( y^{2}-0,25=1 \)

\( y^{2}=1,25 \) 

Der Berührpunkt \(B(0,5|  \sqrt{1,25})\)    \(B(0,5| ≈1,12)\) liegt am nächsten zu \(Q(1|0) \)