Für welchen Radius r wird die Fläche maximal? (Optimierung der Laufbahn der Bezirkssportanlage)

Question

Das Stadion der Bezirkssportanlage besteht aus einer rechteckigen Fläche mit den Kanten a und b, wobei a < b, und aus zwei gleichen an a anliegenden Halbkreisen, deren Radius also a÷2 ist. (siehe Bild)

Die Laufstrecke setzt sich aus 2xb und dem (halben) Umfang der Halbkreise zusammen und ist 400m lang.

Für welchen Radius r wird die Fläche maximal?

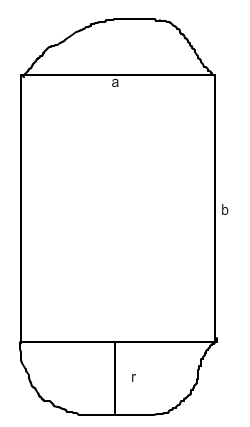
Mein Ansatz:

Hauptbedingung: A=a*b=2r*b

Nebenbedingung: U_ges=400m=2πr+2b

                            b=200m-πr

Zielfunktion: A(r)=2r*(200m-πr)

                A(r)=400m*r-2πr²

                A'(x)=400m-4πr

                A''(x)=(-4π)

A'(x)=0

0=400m-4πr

r=100π

A''(100π)=(-4π) < 0 -> lokales Maximum

-> für Radius 100 π ist A maximal

Das kann doch nicht stimmen oder?

Welcher Bezirkssportanlagenplatz ist denn 628m breit?!?!

Ich würde mich freuen, wenn mir jemand eine detaillierte Lösung zeigen könnte, die genauso aufgebaut ist, wie mein Ansatz, also mit HB, NB & ZF.... Am besten gleich dazusagen, wo mein Denkfehler liegt.

Answer 1

An sich ist alles richtig, aber am Ende hast Du Dich vertan:

0=400m-4πr

r=100/π

 

Du musst durch π teilen. Steht ja vorerst noch beim r ;).