Aufgabe (Doppelintegrale in Polarkoordianten):
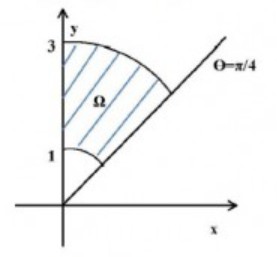
Berechnen Sie das Volumen über der in der Skizze dargestellten Bodenfläche \( \Omega \) unter der Bildfläche der durch \( z=f(x ; y)=x^{2} y \) gegebenen Funktion.
Tipp: \( \int \cos ^{2} x \cdot \sin x d x=-\frac{\cos ^{3} x}{3}+c \) (Papula Formelsammlung, Integralnummer 256)
Ansatz/Problem:
Meine Rechnung:
\( z=f(x, y)=x^{2} y \)
\( x=r \cdot \cos \varphi \quad y=r \cdot \sin \varphi \)
\( 1 \leq r \leq 2 ; \quad 0 \leqslant \varphi \leqslant \frac{\pi}{4} \)
\( \int \limits_{0}^{\frac{\pi}{4}} \int \limits_{1}^{2} r^{2} \cos ^{2} y \cdot r \cdot \sin \varphi \cdot r \cdot d r \cdot d y \)
innen \( \int \limits_{1}^{2} r^{4} \cos ^{2} \varphi \sin \varphi d r=\left[\frac{1}{5} r^{-2} \cos ^{2} \varphi \sin \varphi\right]_{1}^{2} \)
\( =\frac{31}{5} \cos ^{2} \varphi \sin \varphi \)
außen \( \quad \frac{31}{5} \int \limits_{0}^{\pi / 4} \cos ^{2} \varphi \sin \varphi=\frac{31}{5}\left[-\frac{\cos ^{3} y}{3}\right]_{0}^{\pi / 4} \)
\( =-\frac{31}{45} \cdot \frac{\sqrt{2}}{4}+\frac{31}{15}=1,336 \)