Aufgabe zu Polarkoordinaten bei mehrdimensionaler Integration:
Bestimmen Sie den Wert des Integrals für den angegebenen Integrationsbereich.
$$ \int \limits_{G}\left(x^{2}+y^{2}\right) d(x, y) \quad G=\left\{(x, y) \in \mathbb{R}^{2}:|x| \geq 1 \text { oder }|y| \geq \frac{1}{2}, x^{2}+y^{2} \leq 4\right\} $$
Skizzieren Sie dazu zuerst den Integrationsbereich \( G . \) Verwenden Sie auch Polarkoordinaten.
Den Integrationsbereich zu skizzieren schaffe ich noch.
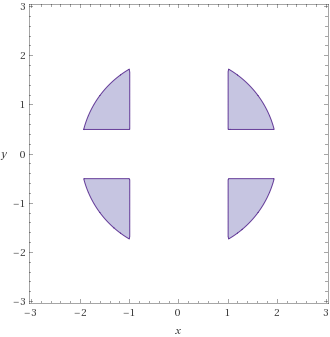
Meine Vorgehensweise wäre es, die Menge G aufzuteilen in G1 (Kreis in Polarkoordinaten): r ∈ [0,2] und φ∈[0,2π],
G2: |x| ≥ 1 und G3: |y| ≥ 0,5 und dann
\( \int\limits_{G1}^{\ } \) f - \( \int \limits_{G2}^{~} \) f - \( \int\limits_{G3}^{~} \) f also praktisch \( \int\limits_{0}^{\ 2π} \)\( \int\limits_{0}^{\ 2} \) f*r dr dφ - \( \int\limits_{-1}^{ 1} \) fdx - \( \int\limits_{-0,5}^{ 0,5} \) fdy zu berechnen.
Ich bin mir aber nun nicht ganz sicher, ob 1. das bei dieser Menge G überhaupt richtig ist und 2. ob ich nicht noch eventuell G1∩G2 auf irgendeine Weise addieren muss, weil ich ja das Rechteck [-1,1]∩[-0,5;0,5] effektiv zweimal abziehe.
Allgemein wirkt mein Vorgehen auf mich im Moment ziemlich falsch.
Würde mich sehr freuen, wenn mir jemand seine Vorgehensweise erläutern könnte.