Berechnen Sie das Volumen über der in der Skizze dargestellten Bodenfläche.

Question

Aufgabe (Doppelintegrale in Polarkoordianten):

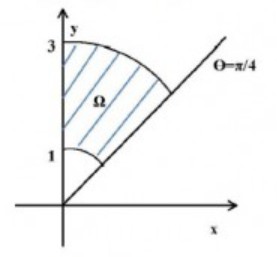
Berechnen Sie das Volumen über der in der Skizze dargestellten Bodenfläche $\Omega$ unter der Bildfläche der durch $z=f(x ; y)=x^{2} y$ gegebenen Funktion.

Tipp: $\int \cos ^{2} x \cdot \sin x d x=-\frac{\cos ^{3} x}{3}+c$ (Papula Formelsammlung, Integralnummer 256)

Ansatz/Problem:

Meine Rechnung:

$z=f(x, y)=x^{2} y$
$x=r \cdot \cos \varphi \quad y=r \cdot \sin \varphi$
$1 \leq r \leq 2 ; \quad 0 \leqslant \varphi \leqslant \frac{\pi}{4}$

$\int \limits_{0}^{\frac{\pi}{4}} \int \limits_{1}^{2} r^{2} \cos ^{2} y \cdot r \cdot \sin \varphi \cdot r \cdot d r \cdot d y$

innen $\int \limits_{1}^{2} r^{4} \cos ^{2} \varphi \sin \varphi d r=\left[\frac{1}{5} r^{-2} \cos ^{2} \varphi \sin \varphi\right]_{1}^{2}$

$=\frac{31}{5} \cos ^{2} \varphi \sin \varphi$
außen $\quad \frac{31}{5} \int \limits_{0}^{\pi / 4} \cos ^{2} \varphi \sin \varphi=\frac{31}{5}\left[-\frac{\cos ^{3} y}{3}\right]_{0}^{\pi / 4}$

$=-\frac{31}{45} \cdot \frac{\sqrt{2}}{4}+\frac{31}{15}=1,336$

Comments

Warum nimmst du nicht phi (oder theta?) von π/4 bis π/2 und r von 1 bis 3?

---

Ach stimmt ja die Intervallgrenzen habe ich falsch gesetzt, das wusste ich doch. Danke :)

Answer 1

Bitte. Gern geschehen.

Mit phi (oder theta?) von π/4 bis π/2 und r von 1 bis 3 sollte das dann wohl klappen.

Musst du zum Schluss nicht den exakten Wert mit Wurzeln... angeben? Rundet ihr da?