Wechselstrom Komplexe Zahlen Widerstandsoperatoren

Question

Ich komme derzeit nicht weiter und beschäftige mich in meinem Lehrbuch mit den Folgenden beiden Aufgaben:

\( \underline{Z}=\frac{R \cdot\left(-j X_{\mathrm{C}}\right)}{R-j X_{\mathrm{C}}}=\frac{-j 100 \Omega \cdot 150 \Omega}{100 \Omega-j 150 \Omega}=\frac{15000 \Omega^{2}\left\lfloor-90^{\circ}\right.}{180,3 \Omega-56,3^{\circ}}=83,2 \Omega\left\lfloor-33,7^{\circ}\right. \)

\( \underline{Z}=\frac{\underline{Z}_{1} \cdot \underline{Z}_{2}}{\underline{Z}_{1}+\underline{Z}_{2}}=\frac{R \cdot\left(-j X_{\mathrm{C}}\right)}{R-j X_{\mathrm{C}}}=\frac{-j 100 \Omega \cdot 150 \Omega}{100 \Omega-j 150 \Omega}=69,2 \Omega-j 46,2 \Omega \)

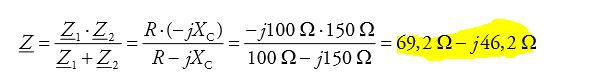
Im Buch ist nicht weiter beschrieben wie die gelbe Markierung berechnet wurde.

Comments

Danke ich habe es jetzt herausgefunden im Zähler wird Multipliziert der winkel wird aus einer Tabelle abgelesen -j = 90° und im Nenner wird der Betrag √100²⁺150² errechnet und aus der Komplexen der Winkel bestimmt.

Answer 1

Bei der ersten Aufgabe wurde einfach die komplexe Impedanz von kartesischer in Polarkoordinatenform gebracht:

Aus $$ a+bj $$ wird $${ r*e }^{ j\varphi  }=r \lfloor  \varphi $$ mit $$r=\sqrt { { a }^{ 2 }+{ b }^{ 2 } } \quad\quad \varphi =arctan\left( \frac { b }{ a }  \right) $$

Bei der zweiten Aufgabe werden 2 komplexe Zahlen miteinander dividiert. Dies ist relativ einfach zu bewerkstelligen wenn man den Bruch mit der komplex Konjugierten des Nenners erweitert. Beispiele dazu gibt es im Internet zuhauf ;)