2.1.1 Zu lösen ist die GLeichung
0 = x³ - 6x² + 12x - 8
Eine Lösung findet man leicht durch Raten: x = 2
Also führt man eine Polynomdiskussion durch:
(x³ - 6x² + 12x - 8) / (x-2) = x² - 4x + 4
x³ - 2x²
-4x² + 12x
-4x² + 8x
4x - 8
4x - 8
0
Gesucht sind also weitere Lösungen von
0 = x² - 4x + 4 = (x-2)²
Also gibt es außer x=2 keine weiteren Lösungen.
2.1.2 Zunächst bestimmt man die erste Ableitung:
f'(x) = 3x² - 12x + 12
Die notwendige Bedingung für einen Extrempunkt lautet
f'(x) = 0
0 = 3x² - 12x + 12
0 = x² - 4x + 4
0 = (x-2)²
Die einzige kritische Stelle für einen Extrempunkt ist also x=2.
Zu prüfen ist nun f''(2): f''(x) = 6x - 12
Also gilt f''(2) = 0, was keine Entscheidung über das tatsächliche Vorliegen eines Extrempunkts zulässt.
Wegen f'''(2) = 6 liegt aber kein Extrempunkt, sondern ein Sattelpunkt vor!
2.1.3 Dieser Punkt ist gleichzeitig der einzige Wendepunkt von f.
2.2 Für x<2 gilt f''(x)<0, also ist die Funktion dort rechtsgekrümmt. Für x>2 gilt f''(x)>0, also ist die Funktion dort linksgekrümmt.
2.3 Wegen f(x) = (x-2)³ ist die Funktion punktsymmetrisch bei Spiegelung am Punkt (2, 0).
2.4 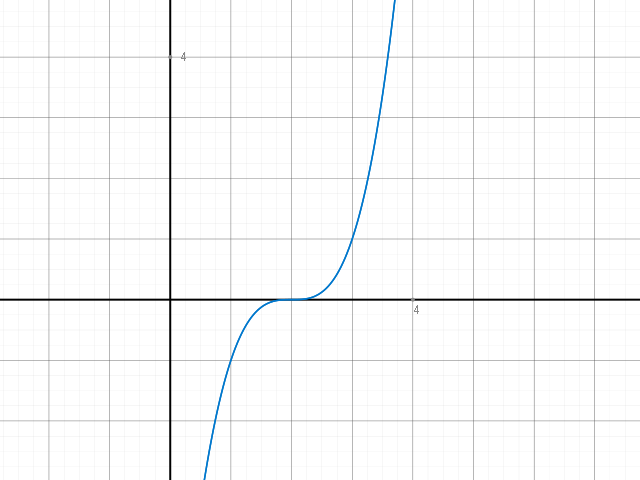
Willst du es mit dieser Aufgabe als Beispiel vielleicht für die andere Aufgabe selbst versuchen?