Hallo :)
f(x) = 1/3 x²-4x
Nullstellen: hier gibt es nen Trick. Du hast nur Terme mit x, also kannst du ausklammern:
x(1/3x²-4) = 0
Also MUSS ein Faktor Null sein. Jetzt musst du jeweils Werte in der Klamer finden, damit der Term in der Klammer null ergibt (Nullprodukt). Jetzt nimmst du dir also diesen Term und bestimmst deren Lösungsmenge. Diese ist dann 1/3x² = 4, also x² = 12 und x = ±√12.. Somit hast du schon mal die NST.
____________________________________________________________________________________
Nun bilden wir die erste Ableitung von f:
f'(x) = x² -4
0 = x²-4 => x² = 4 => x = ±2
Also sind die Extremstellen E12 = 2 und E2 = -2.
Für die Art bestimmen wir nun f''(x):
f''(x) = 2x
Das erste ist somit ein Tiefpunkt, das zweite ein Hochpunkt nach Definition:
f''(e) > 0 => Tiefpunkt
f''(e) < 0 => Hochpunkt
__________________________________________________________________________________
Wendepunkt: (0|0)
=> in f'(x) eingesetzt sieht man, dass die Steigung m = -4 ist.
Das Einsetzen von WP und m in t(x) = mx+b ergibt t(x) = -4x.
___________________________________________________________________________________
Schau dir dies mal an, das ist das Bild, was in Aufgabe 4 entsteht:
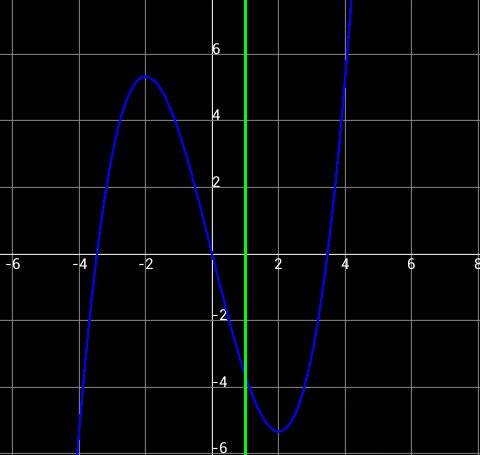
Das blaue ist dein Graph, das Grüne x=1. der vierte Quadrant ist unten rechts. Abszisse ist die x-Achse. Da siehst du auch diese eingeschlossene Fläche. Du musst also das Integral von 0 bis 1 von f(x) berechnen:
F(x) = 1/12x4 -2x²
0∫1(f(x)) dx = [0] - [1/12-2] = -1,92 => Betrag nehmen, also A = 1,92 FE (Flächeneinheiten).
___________________________________________________________________________________
Ich hoffe das hat etwas geholfen, bei Fragen melde dich :)