Aufgabe:
Welche Matrix projiziert den durch die Einheitsvektoren in \( \mathrm{R}^{3} \) aufgespannten Einheitswürfel so in die Ebene, dass dieses Bild in \( \mathrm{R}^{2} \) entsteht:
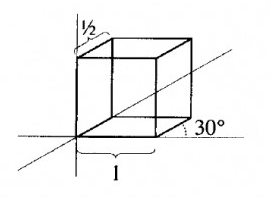
Die Lösung dazu lautet:
Dann gilt für die Einheitsvektoren: \( \left(\begin{array}{l}1 \\ 0 \\ 0\end{array}\right) \mapsto\left(\begin{array}{l}1 \\ 0\end{array}\right),\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right) \mapsto\left(\begin{array}{c}0 \\ 1\end{array}\right),\left(\begin{array}{l}0 \\ 1 \\ 0\end{array}\right) \mapsto\left(\begin{array}{c}\sqrt{3} / 4 \\ 1 / 4\end{array}\right) \)
Und wir haben die Matrix für diese Parallelprojektion \( A=\left(\begin{array}{ccc}1 & \sqrt{3} / 4 & 0 \\ 0 & 1 / 4 & 1\end{array}\right) \).
Ansatz/Problem:
Ich verstehe nun nicht ganz, wie diese Abbildungen zustande gekommen sind. Zumal auf dem Bild ja nicht der R², sondern der R³ ist, oder?