Also, mal ausgehend von Unkowns Bild:
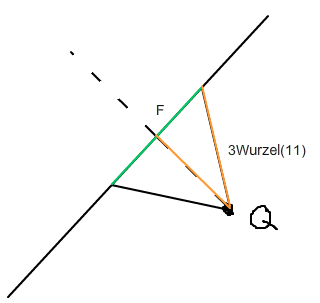
Die kürzeste Verbindung zwischen g und Q steht senkrecht auf g! Das ist eine allgemeine Tatsache im Raum, die man z.B. mit der Differentialrechnung zeigen kann.
Darum bildet man die Ebene E, die senkrecht auf g steht und durch Q geht, denn alle Vektoren innerhalb der Ebene stehen nun senkrecht auf g. Dann berechnet man den Schnittpunkt von E und g, das ist dann der Punkt auf g, der Q am nächsten liegt.
Im Bild ist das der Punkt F. Dann kann die grüne Strecke mit dem Satz des Pythagoras bestimmt werden.
E bestimmt man zum Beispiel mit der Normalenform:
E: (x - a) * n = 0
wobei n der Normalenvektor und a der Stützvektor der Ebene sind. Mit
n = (1|2|2)
a = (9|12|-2)
steht die Ebene also senkrecht auf g und geht durch Q.
Damit erhält man ausmultipliziert die Koordinatendarstellung von E:
x*n - a*n = 0
Der Vektor x hat die Koordinaten (x|y|z), also ist diese Gleichung ausmultipliziert:
x + 2y + 2z - 9 - 24 + 4 = 0
x + 2y + 2z = 29
Wenn man nun die Parameterform von g in ihre einzelnen Komponenten auffächert, erhält man:
x = 2 + r
y = 1 + 2r
z = -1 + 2r
was man für die Schnittpunktsberechnung einfach in die Koordinatenform der Ebene einsetzt:
(2+r) + 2*(1+2r) + 2*(-1 + 2r) = 29
2 + r + 2 + 4r - 2 + 4r = 29
9r = 27 |:9
r = 3
Also erhält man für den Ortsvektor OF des Schnittpunkts:
OF = (2|1|-1) + 3*(1|2|2) = (5|7|5)
Und der Abstandsvektor zwischen OT und Q ist
d = (5|7|5) - (9|12|-2) = (-4| -5| 7)
Mit dem Betrag:
d² = 16 + 25 + 49 = 90
Mit dem Satz des Pythagoras erhält man nun für den Abstand s der gesuchten Punkte von F:
3*√11 = √(d² + s²)
99 = d² + s²
99 = 90 + s²
s² = 9
s = 3
Da der Richtungsvektor von g, (1|2|2) selber die Länge 3 hat, sind die gesuchten Punkte also
P1/2 = (5|7|5) ± (1|2|2)
P1 = (6|9|7)
P2 = (4|5|3)
Aufgabe 2:
Das ist sehr einfach, weil wir ja schon die orthogonale Projektion von Q(9|12|-2) auf g berechnet haben, nämlich den Punkt F(5|7|5).
Man erhält nun den gespiegelten Punkt, indem man einfach denselben Weg nocheinmal zurücklegt, also gemäß
OQ1 = OF + (OF - OQ)
(Wenn ich ein O vor den Punkt setze, meine ich immer den Ortsvektor.)
Man erhält:
OQ1 = (5|7|5) + ((5|7|5) - (9|12|-2))
OQ1 = (1|2|12)