Funktionen - Parabel 2. Ordnung. Brückendurchfahrt für Fahrzeug.

Question

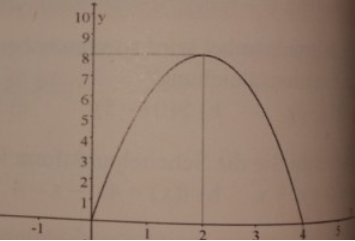
Die Brückendurchfahrt hat die Form einer Parabel 2. Ordnung (siehe Abb.). Bestimmen Sie die Funktionsgleichung. Ein Fahrzeug ist 3 m breit und 3 m hoch, ein anderes 3,25 m breit und 3 m hoch. Untersuchen Sie, ob beide Fahrzeuge die Brücke unterqueren können.

war leider schon immer eine Niete in der Mathematik und bräuchte mal von einem netten Helfer einen kleinen Anstupser bei einer Aufgabe, welche ich als Bild darstelle.

Da es sich hierbei um eine Parabel 2. Ordnung handelt, wissen wir ja, dass die Funktionsgleichung wie folgt lautet: f(x)= a*x^2+bx+c

Hier angekommen weiß ich auch schon nicht mehr wirklich weiter. Ein kleiner Tipp wäre super :-)

Danke Euch :-)

Answer 1

Ausgehend von

f ( x ) = -2x^2 + 8x

Der Lkw fährt mittig durch den Tunnel
Bei 3 m Breite ist
die linke Seite bei 2 - 1.5 = 0.5 m
der rechte Seite bei 2 + 1.5 m = 3.5 m

Der Funktionswert ( Höhe )  ist
f ( 3.5 ) = -2 * 3.5^2 + 8 * 3.5
f ( 3.5 ) = -24.5 + 28 = 3.5 m

Der Lkw hat eine Höhe von 3 m. Er kann den Tunnel durchfahren.

Mit 3.25 m genauso verfahren.

Answer 2

f(x)=ax²+bx,  da Ursprungsfunktion.

I.  f(2)=8       4a+2b=8

II. f´(2)=0      4a+b=0

Man erhält b=8 und a=-2

f(x)=-2x²+8x

Den Rest kannst du sicherlich selbst lösen.

LG

Comments

Hi Simon,

vielen Dank erstmal für die schnelle Antwort. Das hat mir jetzt allerdings nicht viel weitergeholfen :(

Ich bin am verzweifeln!!!

---

Anders ausgedrückt: ich kann nicht wirklich nachvollziehen, wie du darauf gekommen bist.

Answer 3

geht die Parabel mit dem Scheitel \((x_s|y_s)\) durch den davon verschiedenen Punkt \((x_p|y_p)\), dann hat sie die Gleichung $$ y=\frac { y_p-y_s }{ \left(x_p-x_s\right)^2 }\cdot \left(x-x_s\right)^2+y_s. $$