Extrema,Wendepunkte f(x)= (-x+2)e^x

Question

f(x)= (-x+2)e^x

Ich weiß nicht wie ich auf die Extrema und wendepunkte komme !

Auch muss ich die schnittpunkte mit der x und y achse herausfinden.

ich hoffe ihr könnt mir helfen :)

Answer 1

f(x) = (-x + 2) * e^x

Schnittpunkt mit der x-Achse:

(-x + 2) * e^x = 0

e^x  ≠ 0 für alle x, also

-x + 2 = 0 | x = 2 | Schnittpunkt mit x-Achse ist also (2|0).

Schnittpunkt mit y-Achse, x = 0 einsetzen:

(-0 + 2) * e⁰ = 2 * 1 = 2 | Schnittpunkt mit y-Achse ist also (0|2).

Extrema, 1. Ableitung = 0, 2. Ableitung ≠ 0.

(uv)' = u'v + uv'

u = -x + 2 | u' = -1

v = e^x | v' = e^x

f'(x) = -1 * e^x + (-x + 2) * e^x = (-x + 1) * e^x

f'(x) = 0 | (-x + 1) * e^x = 0 | x = 1

(uv)' = u'v + uv'

u = -x + 1 | u' = -1

v = e^x | v' = e^x

f''(x) = -1 * e^x + (-x + 1) * e^x = -x * e^x

f''(1) = -1 * e^-1 < 0, also liegt an der Stelle x = 1 ein Maximum vor.

f(1) = (-1 + 2) * e¹ = e

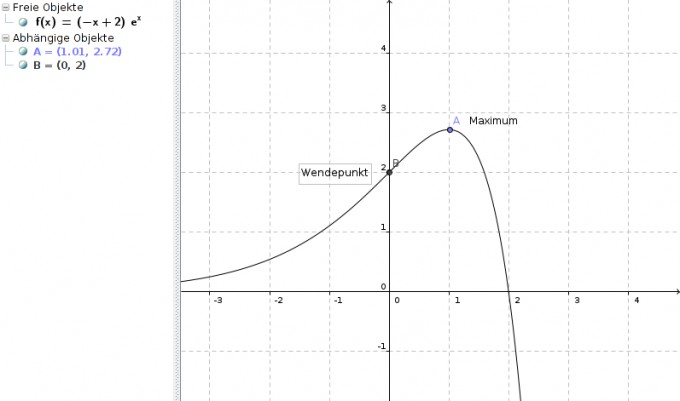
Wir haben also ein Maximum im Punkt (1|e).

Wendepunkt: f''(x) = 0, f'''(x) ≠ 0

f''(x) = -x * e^x = 0 | x = 0

(uv)' = u'v + uv'

u = -x | u' = -1

v = e^x | v' = e^x

f'''(x) = -1 * e^x + (-x) * e^x = (-x - 1) * e^x

f'''(0) = -1 * e⁰ = -1 * 1 = -1 ≠ 0

Also haben wir an der Stelle x = 0 einen Wendepunkt

f(0) = (-0 + 2) * e⁰ = 2 * 1 = 2

Wendepunkt (0|2)

 

Besten Gruß

Comments

Sehr gern geschehen!

War zwar ziemlich rechenaufwändig, hat aber irgendwie Spaß gemacht :-D

---

Das geht auch deutlich weniger aufwändig, angefangen bei den Ableitungen ist

\( f(x)= (-x+2)\cdot\text{e}^x \)

\( f'(x)= (-x+1)\cdot\text{e}^x \)

\( f''(x)= (-x+0)\cdot\text{e}^x \)

\( f'''(x)= (-x-1)\cdot\text{e}^x \)

usw. und damit folgt durch Ablesen und Einsetzen:

Schnittpunkt mit der \(y\)-Achse und einziger Wendepunkt: \((0\,|\,2)\)
einziger Schnittpunkt mit \(x\)-Achse: \((2\,|\,0)\)
Hoch- und einziger Extrempunkt: \((1\,|\,\text{e})\)

Insbesondere beim Ableiten lässt sich oft Arbeit einsparen.

---

Das ist sehr elegant und zeitsparend - hätte ich aber offengestanden so nicht gesehen.

Danke sehr!