Question

Bestimmen Sie alle lokalen Extrema und alle Wendepunkte der Funktion f(x) = 2e^2x - 4x
Bestimmen Sie jeweils die Art der lokalen Extrema und Wendepunkte.

 

Wie kann man das machen ?

Comments

'-4x' definitiv nicht im Exponenten?

---

Sorry, es gibt ein Fehler es ist f(x) = 2e^2x - 4e^x.

Answer 1

f(x) = 2·e^{2·x} - 4x
f'(x) = 4·e^{2·x} - 4
f''(x) = 8·e^{2·x}

Extrempunkte f'(x) = 0
4·e^{2·x} - 4 = 0
e^{2·x} = 1
x = 0

f(0) = 2
f''(0) = 8 > 0 --> Tiefpunkt

Wendepunkte f''(x) = 0

8·e^{2·x} = 0
Die e-Funktion wird nie null, daher gibt es hier keine Wendepunke.

Skizze:

Comments

Entschuldigung für meinen Fehler. Es muss so sein.

 

f(x)  = 2e^2x - 4e^x

---

f(x) = 2·e^{2·x} - 4·e^x = 2·e^x·(e^x - 2)

f'(x) = 4·e^{2·x} - 4·e^x = 4·e^x·(e^x - 1)

f''(x) = 8·e^{2·x} - 4·e^x = 4·e^x·(2·e^x - 1)

Das sind jetzt die notwendigen Ableitungen. Den Rest schaffst du sicher selber.

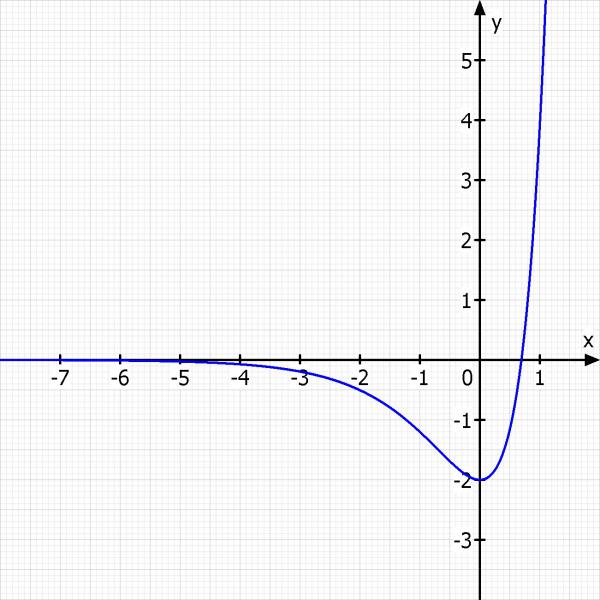
Hier noch eine Skizze zum Überprüfen der Lösungen:

---

Ich verstehe nicht so gut die Extrem- und Wendepunkte. Wirste bitte mal bis zum Ende machen ?

---

f(x) = 2·e^2·x - 4·e^x = 2·e^x·(e^x - 2)
f'(x) = 4·e^2·x - 4·e^x = 4·e^x·(e^x - 1)
f''(x) = 8·e^2·x - 4·e^x = 4·e^x·(2·e^x - 1)

Ist ja immer das gleiche

Extrempunkte f'(x) = 0
4·e^x·(e^x - 1) = 0
e^x - 1 = 0
x = ln(1) = 0

f(0) = -2

Tiefpunkt laut Skizze

Wendepunkte f''(x) = 0

4·e^x·(2·e^x - 1) = 0
2·e^x - 1 = 0
x = ln(1/2) = -0.6931471805

f(ln(1/2)) = -3/2

Das war es dann auch schon.